- Research article
- Open access
- Published:
Simulation-based model checking approach to cell fate specification during Caenorhabditis elegans vulval development by hybrid functional Petri net with extension
BMC Systems Biology volume 3, Article number: 42 (2009)
Abstract
Background
Model checking approaches were applied to biological pathway validations around 2003. Recently, Fisher et al. have proved the importance of model checking approach by inferring new regulation of signaling crosstalk in C. elegans and confirming the regulation with biological experiments. They took a discrete and state-based approach to explore all possible states of the system underlying vulval precursor cell (VPC) fate specification for desired properties. However, since both discrete and continuous features appear to be an indispensable part of biological processes, it is more appropriate to use quantitative models to capture the dynamics of biological systems. Our key motivation of this paper is to establish a quantitative methodology to model and analyze in silico models incorporating the use of model checking approach.
Results
A novel method of modeling and simulating biological systems with the use of model checking approach is proposed based on hybrid functional Petri net with extension (HFPNe) as the framework dealing with both discrete and continuous events. Firstly, we construct a quantitative VPC fate model with 1761 components by using HFPNe. Secondly, we employ two major biological fate determination rules – Rule I and Rule II – to VPC fate model. We then conduct 10,000 simulations for each of 48 sets of different genotypes, investigate variations of cell fate patterns under each genotype, and validate the two rules by comparing three simulation targets consisting of fate patterns obtained from in silico and in vivo experiments. In particular, an evaluation was successfully done by using our VPC fate model to investigate one target derived from biological experiments involving hybrid lineage observations. However, the understandings of hybrid lineages are hard to make on a discrete model because the hybrid lineage occurs when the system comes close to certain thresholds as discussed by Sternberg and Horvitz in 1986. Our simulation results suggest that: Rule I that cannot be applied with qualitative based model checking, is more reasonable than Rule II owing to the high coverage of predicted fate patterns (except for the genotype of lin-15ko; lin-12ko double mutants). More insights are also suggested.
Conclusion
The quantitative simulation-based model checking approach is a useful means to provide us valuable biological insights and better understandings of biological systems and observation data that may be hard to capture with the qualitative one.
Background
Model checking is a successful method for automatic verification of software and reactive systems [1], which is usually applied to ensure consistency and correctness of designed models. Practiced verification methods in most cases are still simple simulation and testing. While simple simulation and testing provide a part of the possible results of a model, model checking can conduct an exhaustive exploration of all possible behaviors [1–4].
Among the features, one merit of using model checking is that it is possible to verify a set of rules defined by users. Recently, the size of targeting network becomes enlarged and difficult to check all rules and their combinations by each user, especially, biologist. To solve this, around 2003, several attempts were launched to apply model checking approaches to biological pathway validations [5–12]. With the aid of model checking approach, one can obtain answers to questions such as "what is the probability that the gene finally expressed?" and "does this reaction always lead to DNA fragmentation?" In 2007, Fisher et al. proved the importance of model checking approach by inferring the new regulation of inductive and lateral signaling crosstalk of C. elegans and confirming the regulation with biological experiments [9]. The approach was applied on a discrete model by using one of the model checking languages named reactive modules [13]. However, quantitative properties (e.g. continuous feature) are also important in biological processes, such as the concentration of proteins and the reaction rates. Thus, it is desirable to deal with both discrete and continuous features in the model (called hybrid model). From this fact, the next challenge is to apply the model checking approach to such hybrid models. Several hybrid models have been applied to biological pathway modeling, e.g. hybrid automata [6], π-calculus [14], ordinary differential equations (ODEs) [15], and hybrid functional Petri nets (HFPN) [16] and its extension (HFPNe) [17, 18]. Among them, HFPNe and its related concepts have been accepted as a formal modeling method due to potential advantages of HFPNe possessing intuitive graphical representation and capabilities for mathematical analysis [19–23].
We use HFPNe to quantitatively model C. elegans vulval development mechanism, which best meets the features of biological processes. We have been developing an HFPNe based software "Cell Illustrator" [24, 25] for modeling and simulating biological pathways [17, 18, 26]. It has been successfully employed to develop and analyze some pathway models for gene regulatory networks, metabolic pathways, and signaling pathways [16, 27–31]. In this paper, Cell Illustrator is used as a software tool to model and simulate this complicated biological system in C. elegans.
The paper is organized as follows: In Methods, we first present an introduction of HFPNe and biological background of VPC fate determination mechanism. We demonstrate how to construct VPC fate model by using HFPNe afterwards. When determining cell fate from biological points of view, several biological fate determination rules can be considered. We thus employ two major biological fate determination rules – Rule I and Rule II – to the VPC fate model. Two rules are used to determine the cell fate from two viewpoints – temporal interval and temporal order – of time course expression of cell fate candidates. Next, we conduct 10,000 simulations for each of 48 sets of different genotypes which are the combination of four mutants and AC (anchor cell). The simulation procedures such as noise parameters, high-speed simulation engine, and the emulation of the temporal stimulations are also described. Finally, we examine the consistency and correctness of the VPC fate model, and evaluate proposed two rules by comparing with three simulation targets consisting of predicted fate patterns obtained from in silico and in vivo experiments. In Results and Discussion, our simulation results suggest that Rule I on the temporal interval is more reasonable than Rule II owing to the high coverage of predicted fate patterns (except for lin-15ko; lin-12ko double mutants), (ii) for the lin-15ko; lin-12ko double mutants, the coverage will be considerably augmented, if the number of animal population is increased in the in vivo experiments, and (iii) unmatched fate patterns of lin-15ko and ac-; lin-15ko, still have the possibility to be examined in in vivo experiments by enlarging animal numbers. More insights concerning the hybrid lineage are also suggested and discussed. The final section concludes the paper and addresses the contributions of the work.
Methods
Figure 1(a) illustrates the procedure overview of Methods. Briefly, starting from an introduction of HFPNe and VPC induction mechanisms, we first show the processes of constructing HFPNe-based VPC fate model (VPC fate model for short). We then employ two major biological fate determination rules to the VPC fate model from different viewpoints: temporal interval and temporal order. Finally, we execute 480,000 simulations in total for different genotypes by comparing with three simulation targets (i.e., JA, ST, and STA) (see Figure 1(b)). JA consists of fate patterns obtained by using model checking approach (with MOCHA); ST is the fate patterns summarized by Sternberg and Horvitz [32]; and STA is the fate patterns derived from [32] including hybrid lineage data. The aims of the simulation are: (i) to investigate predicted fate patterns variations of each genotype, and (ii) to evaluate two rules employed to VPC fate model.
Modeling biological pathways with hybrid functional Petri net with extension (HFPNe)
Brief introduction of HFPNe: an enhanced Petri net for modeling biological interactions
Petri net is a network which consists of place, transition, arc, and token. A place can hold tokens as its content. A transition has arcs coming from places and arcs going out from the transition to some places. A transition with these arcs defines a firing rule in terms of the contents of the places where the arcs are attached [33].
Due to the limitation of conventional Petri net and more requirements in modeling, Matsuno et al. have defined hybrid functional Petri net (HFPN for short) in 2003 [16]. However, when modeling biological pathways, it has been noticed that several useful extensions should be applied for modeling and simulating more complicated biopathway processes (e.g., activities of enzymes for a multi-modification protein) and other biological processes that are not normally treated in biological pathways (e.g., alternative splicing and frameshifting) [18]. Therefore, Nagasaki et al. have proposed a new enhanced Petri net architecture hybrid functional Petri net with extension (HFPNe) in 2004. They have firstly used the new terminology in HFPNe to bridge the gap between the researchers of computer science and biology. In other words, the terms of place, transition, arc, and token are named as entity, process, connector, and content respectively.
HFPNe can deal with three types of data – discrete, continuous, and generic – and comprises three types of elements – entities, processes, and connectors – whose symbols are illustrated in Figure 2. A discrete entity holds a positive integer number of content. A discrete process is the same notion as used in the traditional discrete Petri net [33]. A continuous entity holds a nonnegative real number as concentration of a substance such as mRNA and protein. A continuous process is used to represent a biological reaction such as transcription and translation, at which the reaction speed is assigned as a parameter. A generic entity can hold various kinds of types including object, e.g., the string of nucleotide base sequence. A generic process can deal with any kind of operations (e.g., alternative splicing and frameshifting) to all types of entities. Connectors are classified into three types: process connector, associate connector, and inhibitory connector. Process connector connects an entity to a process or vice versa. Associate or inhibitory connector represents a condition and is only directed from an entity to a process. Each of process connector from an entity, associate connector, and inhibitory connector has a threshold by which the parameter assigned to the process at its head is controlled. A process connector from an entity or an associate connector (an inhibitory connector) can participate in activating (repressing) a process at its head, as far as the content of an entity at its tail is over the threshold. For either of associate or inhibitory connectors, no amount is consumed from an entity at its tail. The followed section only gives the mathematic definitions of HFPNe. For the detailed formal definition and properties of HFPNe, the readers are suggested to refer to [18].
Basic elements of HFPNe and examples of biological icons in Cell Illustrator. In Cell Illustrator [24–26], HFPNe elements are replaced with the biological icons defined in the Cell System Ontology [47]. This replacement makes the HFPNe model of a biological pathway more comprehensible (see [17] for details).
Basic definitions of HFPNe
For modeling complex biological processes intuitively, we are required to deal with various kinds of biological information, e.g. the density of molecules, the number of molecules, sequences, molecular modifications, binding location, localization of molecules, etc. To cope with this feature in biological system modeling, we introduce types for biological entities and processes.
The set T of types is defined by the following abstract syntax:

Then, for θ ∈ T, we define the domain D(θ) of θ as follows:
-
1.
D(boolean) = {true, false}, D(integer) = Z (the set of integers), D(integer+) = N (the set of nonnegative integers), D(real) = R (the set of real numbers), D(real+) = R≥0(the set of nonnegative real numbers), D(string) = S (the set of strings over some alphabet).
-
2.
D(pair(θ1, θ2)) = D(θ1) × D(θ2).
-
3.
D(listθ) = ∪k ≥ 0D(θ)k.
-
4.
D(object(θ1, ⋯, θ n )) = D(θ1) × ⋯ × D(θ n ).
For convenience, we denote D* = ∪θ ∈ TD (θ).
Let E be a finite set. A type function for E is a mapping τ: E → T. For e ∈ E, τ(e) is called the type of e. A marking of E is a mapping M : E → D* satisfying M(e) ∈ D(τ(e)) for e ∈ E. For e ∈ E, M(e) called the mark of e. We denote by ℳ the set of all markings of E. We can regard ℳ as the set ∏e∈ED(τ(e)).
Consider a function f : ℳ → R. For a subset F ⊆ E and an element v ∈ ∏e ∈ FD(τ(e)), let f [F = v]: ∏e ∈ E-FD(τ(e)) → R be the function obtained from f by restricting the value for F to v, i.e. f [F = v](z) = f(z, v) for z ∈ ∏e ∈ E-FD(τ(e)). Let F be a subset of E such that e ∈ F satisfies D(τ(e)) = R or R≥ 0. We say that the function f is continuous for F if f [E - F = v]: ∏e ∈ FD(τ(e)) → R is continuous on ∏e ∈ FD(τ(e)) for any v ∈ ∏e ∈ E-FD(τ(e)).
Based on the above terminology, we define the notion of hybrid functional Petri net with extension (HFPNe). The basic idea of HFPNe is two-fold. The first is to introduce types with which we can deal with various data types. The second is to employ functions of marking f(M) to determine the weight, delay, and speed, etc. which control the system behavior. In the following definition, we use different names instead of place, transition, arc, etc. which are conventionally used in Petri net theory since biological system modeling requires more intuitive names for representing biological entities and processes.
[Definition 1] We define a hybrid functional Petri net with extension (HFPNe) H = (E, P, h, τ, C, d, α) as follows:
-
1.
E = {e1, ⋯, e n } is a non-empty finite set of entities and P = {p1, ⋯, p m } is a non-empty finite set of processes, where we assume E ∩ P = ∅.
-
2.
h : E ∪ P → {discrete, continuous, generic} is a mapping called the hybrid function. Terms "discrete" and "continuous" correspond to those in hybrid Petri net [16] and "generic" is a newly introduced name which can be of any type in T. A process p ∈ P with h(p) = discrete (resp., continuous, generic) is called a discrete process (resp., continuous process, generic process). An entity e ∈ E with h(e) = discrete (resp., continuous, generic) is called a discrete entity (resp., continuous entity, generic entity).
-
3.
τ: E → T is a type function for E such that τ(e) = integer+ if e is a discrete entity, and τ(e) = real+ if e is a continuous entity.
-
4.
C = (EP, PE, a, w, u) consists of subsets EP ⊆ E × P and PE ⊆ P × E. An element in EP ∪ PE is called a connector. Each connector has a connector type which is given by a mapping a : EP ∪ PE → {process, associate, inhibitor} called the connector type function which satisfies the conditions: (i) a(c) = process for c ∈ PE. (ii) All connectors c = (e, p) ∈ EP satisfy the conditions in Table 1(a) and all connectors c = (p, e) ∈ PE satisfy the conditions in Table 1(b). A connector c = (e, p) ∈ EP is called a process connector (resp., an associate connector, an inhibitory connector) if a(c) = process (resp., associate, inhibitor). "Process connector", "associate connector" and "inhibitory connector" correspond to normal arc, test arc and inhibitory arc, respectively. For a connector c = (p, e) ∈ PE, a(c) = process by definition and we also call it a process connector. We say that a connector c = (e, p) ∈ EP is discrete (resp., continuous, generic) if p is a discrete process (resp., continuous process, generic process). In the same way, we also say that c = (p, e) ∈ PE is discrete (resp., continuous, generic) if p is a discrete process (resp., continuous process, generic process). Let ℳ be the set of all markings of E and let F be the set of continuous entities in E. Then we denote
 = {f |f : ℳ → N},
= {f |f : ℳ → N},  = {f |f : ℳ → R≥ 0is continuous for F},
= {f |f : ℳ → R≥ 0is continuous for F},  = {f |f : ℳ → D*}, and
= {f |f : ℳ → D*}, and  = {f |f : ℳ → {true, false}}.
= {f |f : ℳ → {true, false}}.
Then w and u are given as follows:
-
(a)
w :
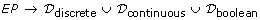 is a function called the activity function such that for a connector c ∈ EP (i) w(c) ∈
is a function called the activity function such that for a connector c ∈ EP (i) w(c) ∈  if c is discrete, (ii) w(c) ∈
if c is discrete, (ii) w(c) ∈  if c is continuous, (iii) w(c) ∈
if c is continuous, (iii) w(c) ∈  if c is generic. For a connector (e, p), w(e, p) be used as a function giving the threshold in discrete and continuous cases and the condition in generic case which is required for enabling the process p.
if c is generic. For a connector (e, p), w(e, p) be used as a function giving the threshold in discrete and continuous cases and the condition in generic case which is required for enabling the process p. -
(b)
u :
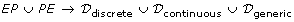 is a function called the update function which satisfies the following conditions: For a connector c ∈ EP ∪ PE, let c = (e, p) ∈ EP or c = (p, e) ∈ PE. (i) u(c) ∈
is a function called the update function which satisfies the following conditions: For a connector c ∈ EP ∪ PE, let c = (e, p) ∈ EP or c = (p, e) ∈ PE. (i) u(c) ∈  if c is discrete. (ii) u(c) ∈
if c is discrete. (ii) u(c) ∈  if c is continuous. (iii) If c is generic, then u(c) is a function in
if c is continuous. (iii) If c is generic, then u(c) is a function in  such that u(c)(M) is in D(τ(e)) for any marking M ∈ ℳ. For a connector c = (e, p) or c = (p, e), u(c) is used as a function which will update the mark of e.
such that u(c)(M) is in D(τ(e)) for any marking M ∈ ℳ. For a connector c = (e, p) or c = (p, e), u(c) is used as a function which will update the mark of e. -
5.
d : Pdiscrete →
 is a mapping called the delay, where Pdiscrete is the set of discrete processes in P. For a discrete process p, d(p): ℳ → R≥0is called the delay function of p.
is a mapping called the delay, where Pdiscrete is the set of discrete processes in P. For a discrete process p, d(p): ℳ → R≥0is called the delay function of p. -
6.
α > 0 is a real number called the generic time. The generic time is used as the clock for generic processes.
We introduce a parameter t ∈ R≥ 0called the time to a hybrid functional Petri net with extension H = (E, P, h, τ, C, d, α). Given a marking I called the initial marking, we define a marking M(t) called the marking at time t and a marking M r (t) called the reserved marking at time t for t ≥ 0 in the following way.
By convention, we denote M(e, t) = M(t)(e) and M
r
(e, t) = M
r
(t)(e) for e ∈ E. We define 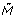 (t) by
(t) by 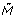 (e, t) = M(e, t) - M
r
(e, t) for discrete and continuous entities and
(e, t) = M(e, t) - M
r
(e, t) for discrete and continuous entities and 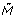 (e, t) = M(e, t) for generic entities e.
(e, t) = M(e, t) for generic entities e.
First, we define M(0) = I, M r (e, 0) = 0 for all discrete and continuous entities e. For all generic entities e, M r (e, t) = null (the empty list) for any t ≥ 0. For t > 0, we define M (t) and M r (t) in the following way.
For a process p ∈ P at time t, if the following conditions are satisfied, then the process p is said to be enabled at time t. Otherwise the process is said to be disabled at time t.
-
1.
If p is a discrete process, then for all connectors c = (e, p) ∈ EP the following conditions hold:
-
(a)
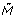 (e, t) ≥ w(e, p)(M(t)) if a(c) ≠ inhibitor.
(e, t) ≥ w(e, p)(M(t)) if a(c) ≠ inhibitor. -
(b)
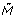 (e, t) <w(e, p)(M(t)) if a(c) = inhibitor.
(e, t) <w(e, p)(M(t)) if a(c) = inhibitor.
-
(a)
-
2.
If p is a continuous process, then for all connectors c = (e, p) ∈ EP the following conditions hold:
-
(a)
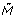 (e, t) ≥ w(e, p)(M(t)) if a(c) ≠ inhibitor.
(e, t) ≥ w(e, p)(M(t)) if a(c) ≠ inhibitor. -
(b)
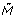 (e, t) ≤ w(e, p)(M(t)) if a(c) = inhibitor.
(e, t) ≤ w(e, p)(M(t)) if a(c) = inhibitor.
-
(a)
-
3.
If p is a generic process, then for all connectors c = (e, p) ∈ EP the following conditions hold:
-
(a)
w(e, p)(
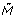 (t)) = true if a(c) ≠ inhibitor.
(t)) = true if a(c) ≠ inhibitor. -
(b)
w(e, p)(
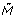 t)) = false if a(c) = inhibitor.
t)) = false if a(c) = inhibitor.
-
(a)
If a disabled process turns to be enabled at time t, the process is said to be triggered at time t. If an enabled process turns to be disabled or a disabled process turns to be enabled at time t, the process is said to be switched at time t. If a discrete process p is triggered at time t, we say that the discrete process can be fired at time t + d(p)(M(t)). If a generic process p is triggered at time t, we say that the generic process can be fired at time t + α.
For an entity e ∈ E and time t, let S d (t) be the set of discrete processes which can be fired at time t, and let U d (t) be the set of discrete processes which are triggered at time t. For a discrete process p that can be fired at time t, we denote by q(p, t) the time when p is triggered. Let S c (t) be the set of continuous processes which are enabled at time t. Let S g (t) be the set of generic processes which can be fired at time t.
Note that we can choose a sufficiently small ε t > 0 such that in the interval [t - ε t , t), neither discrete nor generic process is triggered or can be fired and no continuous process is switched.
Also note the following facts:
-
1.
S c (t - ε t ) = S c (t') for any t' ∈ [t - ε t , t) since no continuous process is switched in the interval [t - ε t , t).
-
2.
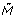 (t') is constant on E - Econtinuous in the interval [t - ε
t
, t) since neither discrete nor generic process is triggered or can be fired in the interval [t - ε
t
, t), where Econtinuous = {e ∈ E |e is continuous}.
(t') is constant on E - Econtinuous in the interval [t - ε
t
, t) since neither discrete nor generic process is triggered or can be fired in the interval [t - ε
t
, t), where Econtinuous = {e ∈ E |e is continuous}. -
3.
For any continuous connector c, u(c)(
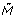 (t')) is continuous on [t - ε
t
, t) since by definition u(c) is continuous for Econtinuous and
(t')) is continuous on [t - ε
t
, t) since by definition u(c) is continuous for Econtinuous and 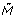 (t') is constant on E - Econtinuous in the interval [t - ε
t
, t).
(t') is constant on E - Econtinuous in the interval [t - ε
t
, t).
Then M(t) is defined by the following procedure:
-
1.
Tmp ← M(t - ε t ), Tmp r ← M r (t - ε t )
-
2.
if t = αk for some integer k ≥ 1 then
for each generic process p ∈ S g (t)
Tmp' ← Tmp
for each (e, p) ∈ EP with a(e, p) = process
Tmp'(e) ← u(e, p)(Tmp)
for each (p, e) ∈ PE
Tmp'(e) ← u(p, e)(Tmp)
Tmp ← Tmp'
-
3.
for each continuous process p ∈ S c (t - ε t )
Tmp' ← Tmp
for each (e, p) ∈ EP with a(e, p) = process

for each (p, e) ∈ PE

Tmp ← Tmp'
-
4.
for each discrete process p ∈ S d (t)
Tmp' ← Tmp
for each (e, p) ∈ EP with a(e, p) = process
Tmp'(e) ← Tmp'(e) - u(e, p)(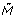 (q(p, t)))
(q(p, t)))
for each (p, e) ∈ PE
Tmp'(e) ← Tmp'(e) + u(p, e)(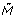 (q(p, t)))
(q(p, t)))
Tmp ← Tmp'
-
5.
M(t) ← Tmp
Then M r (t) is defined as follows:
-
6.
for each entity e with h(e) = discrete or continuous

-
7.
M r (t) ← Tmp r .
We call M(t) (t ≥ 0) the behavior of H starting at the initial marking M(0) = I. □
In the next section, we will introduce the biological background and explain the modeling method of C. elegans vulval development mechanisms.
Biological background and modeling of C. elegans vulval development
Biological background of C. elegans vulval development
The C. elegans vulva is an egg-laying organ which is constituted by the descendants of three VPCs. The three VPCs are the members of six initially equivalent VPCs that are consecutively numbered P3.p – P8.p (termed Pn.p cells). In response to extracellular signaling pathways, each VPC has a potential to adopt one of three alternative cell fates (1°, 2°, 3°) (see Figure 3(a)). Six cell fates of Pn.p cells comprise a cell fate pattern in the form of [P3.p P4.p P5.p P6.p P7.p P8.p]. In wild-type worms, P3.p – P8.p always adopt a same pattern of fates (i.e., [332123]). The sublineage is then generated according to each specified VPC fate. The sublineage is a determined pattern of cell divisions which produces a characteristic set of progeny cell types. Figure 3(b) shows the sublineage of respective VPC fate according to the criteria defined by Sternberg and Horvitz [32].
Schematic representations of VPC fate specification in wild-type hermaphrodites. (a) The anchor cell produces a graded inductive signal and causes six equivalent cells to adopt fates in a precise pattern. (b) The sublineage is generated according to each specified cell fate. The sublineage is a determined pattern of cell divisions which produces a characteristic set of progeny cell types. Sternberg and Horvitz have defined vulval cell types (after two rounds of VPC divisions) by two criteria as follows: the axis of the third round nuclear divisions (L, longitudinal axis; T, transverse axis; N, no division; S is to join the large hypodermal syncytium (hyp7)), and adherence to the ventral cuticle [32].
In wild-type C. elegans, an inductive signal LIN-3, an EGF-like signal produced by gonad, activates the EGFR homolog LET-23 and a canonical Ras/MAPK cascade in P6.p adopting the 1° fate. In response to the inductive signal, P6.p produces LIN-12-mediated lateral signals (LS for short) that counteract the inductive signal from AC in two neighboring VPCs, which causes two VPCs to adopt the 2° fate. In other words, LS induces the expression of negative regulators (collectively termed lateral signal target (lst) genes [34]) against the EGF/Ras/MAPK pathway. LS is encoded by three functionally redundant members of the Delta/Serrate protein family (dsl-1, apx-1, and lag-2) and transduced by the LIN-12/Notch receptor. Each lst gene contains a cluster of binding site LBSs for LAG-1 that is a DNA binding protein forming a complex with the LIN-12 intracellular domain to activate the transcription of the target genes [34–36]. Furthermore, two functionally redundant synthetic Multivulva (synMuv) genes transcriptionally repress the target gene of lin-3 in the hypodermis, i.e., synMuv genes prevent the surrounding hypodermal syncytium hyp7 from generating inductive LIN-3 signals [37]. Without the activation of either inductive or lateral signaling pathways, P3.p, P4.p, and P8.p adopt the 3° fate [35]. Thus, the fates of 1°, 2°, and 3° are the productions of the coordination regulated by three signaling pathways, i.e., AC induced signaling pathways, the lateral signaling pathways, and the signaling pathways induced from hyp7 [32, 35, 38–41]. Figure 4 illustrates the biological diagram for the multiple signaling events underlying the VPC fate specification.
Biological diagram for the multiple signaling events underlying VPC specification. Biological diagram for the multiple regulatory signaling pathways underlying VPC fate specification. Three VPCs (they can be P6.p, P7.p and P8.p, or P6.p, P5.p and P4.p) according to the relative distance to the AC are selected to depict the signaling crosstalk. In the rightmost cell, the EGF/MAPK pathway cannot be activated because the induced signal (indicated by a grey line) received by LET-23, is lower than the threshold for induction, and the VPC hence adopts the 3° fate. The induction signal with high concentration (indicated by a heavy black line) activates the EGF/MAPK pathway and causes the 1° fate. It also has been known that two transcription factors, LIN-31 and LIN-1 are likely to be the downregulation targets of the MAPK pathway [42]. Both LIN-31 and LIN-1 can be phosphorylated by MAPK kinase MPK-1. LIN-31 and LIN-1 usually form a complex that is disrupted by the phosphorylation of LIN-31, and LIN-1 dissociates from LIN-31 to let LIN-31 play a role in the proper specification of VPCs. On the other hands, ligands for LIN-12 are members of the "DSL" family, an acronym derived from canonical ligands from Drosophila (D elta, S errate) and C. elegans (L AG-2). Binding of DSL ligands to LIN-12/Notch leads to the shedding of the LIN-12/Notch ectodomain (extracellular domain) via cleavage. The remaining transmembrane protein is cleaved constitutively, and the intracellular domain translocates to the nucleus, binding to the LAG-1 that usually exists as a transcription factor to repress lst genes. With the binding to LAG-1, lst genes expresses LST proteins to counteract the operations of EGF/MAPK pathways by inhibiting VPCs from becoming the 1° fate. For the details of LIN-12/Notch signaling in C. elegans, the readers are suggested to refer to [34].
Modeling VPC fate specification mechanisms with HFPNe based on literature
Figure 5 exhibits a whole HFPNe based VPC fate model that is constructed by compiling and interpreting the information appeared in the literature concerning the VPC fate specification mechanisms [9, 32, 34–38, 42–46]. The whole VPC fate model totally includes 427 entities, 554 processes and 780 connectors. The elements of HFPNe are changed to biological icons in Cell Illustrator (on the right side of Figure 2). The icons have been defined with one of the biological ontology information, called Cell System Ontology [47]. Although these changes have no effect on mathematical meaning, it is helpful for biologists to understand the pathways.
Since six VPCs are initially equivalent, we hereafter explain modeling operations by using a single VPC fate model as shown in Figure 6 whose six copies are embedded in the whole VPC fate model in Figure 5. In Figure 6, 24 events directly attending VPC fate specification are assigned to the processes p
i
∈ {p 1, ⋯, p24} (see Table 2). A set of sink processes  denotes the natural degradation of the substances, whereas a set of source processes
denotes the natural degradation of the substances, whereas a set of source processes  denotes the translation reactions of initial entities. The left 13 processes {p25, p26, ⋯, p37} are generic processes, which contribute to play the roles of extracellular stimuli ({p 25}) and the cell fate specification ({p26, p27, ⋯, p37}). Variable m
x
∈ {m1, ⋯, m32} denotes the concentration of corresponding substance (see Table 3).
denotes the translation reactions of initial entities. The left 13 processes {p25, p26, ⋯, p37} are generic processes, which contribute to play the roles of extracellular stimuli ({p 25}) and the cell fate specification ({p26, p27, ⋯, p37}). Variable m
x
∈ {m1, ⋯, m32} denotes the concentration of corresponding substance (see Table 3).
HFPNe model of a single VPC in Figure 5. The naming rules of the VPC fate model are defined as follows: (i) each "entity" is labeled with the name of a substance (e.g. LIN-3, LET-60, and lst gene), (ii) the name of a complex consisting of two or more protein components A1, A2, ⋯, A M (M ∈ Z+) is represented as A1 _A2_ ⋯ _A M , and (iii) an additional label (C) or (N) is attached at the end of a substance name, when it happens to distinguish the location of the substance in the cytoplasm or the nucleus. The label of {active} denotes the active state of the enzyme, and {p} denotes that the substance is phosphorylated.
The modeling operation starts from the source process  denoting an activity that the substance takes part in the reaction. Here we only explain the case of Ras/MAPK inductive signaling pathway: LIN-3 ligands and corresponding receptors LET-23 are assigned to the entities (m1 and m2) connected from the source processes (
denoting an activity that the substance takes part in the reaction. Here we only explain the case of Ras/MAPK inductive signaling pathway: LIN-3 ligands and corresponding receptors LET-23 are assigned to the entities (m1 and m2) connected from the source processes ( and
and  ), respectively. Next, the ligand-receptor binding reaction where two entities (m1 and m2) merge into an entity m3 denoting ligand-receptor complex is represented via the process p3. Since two ligand-receptor complexes shape a dimer, the process p4 is used to represent the homodimerization connecting from the input entity m3 as well as connecting to the output entity m4 of LIN-3/LET-23 dimer. Note that the stoichiometry of the input connector of p4 is set to 2 due to the dimerization. The dimer is autophosphorylated subsequently which is modeled by using a phosphorylation process p5 connecting from and to the entities of m4 and m5, respectively. Succedent reactions for the products of the canonical cascades: active SEM-5 (m7), LET-60 (m9), and MPK-1 (m11) are modeled in the same way using the processes of activation (p6, p7 and p8). Activated MPK-1 then moves from the cytoplasm to the nucleus. This movement is modeled as a translocation reaction by p9.
), respectively. Next, the ligand-receptor binding reaction where two entities (m1 and m2) merge into an entity m3 denoting ligand-receptor complex is represented via the process p3. Since two ligand-receptor complexes shape a dimer, the process p4 is used to represent the homodimerization connecting from the input entity m3 as well as connecting to the output entity m4 of LIN-3/LET-23 dimer. Note that the stoichiometry of the input connector of p4 is set to 2 due to the dimerization. The dimer is autophosphorylated subsequently which is modeled by using a phosphorylation process p5 connecting from and to the entities of m4 and m5, respectively. Succedent reactions for the products of the canonical cascades: active SEM-5 (m7), LET-60 (m9), and MPK-1 (m11) are modeled in the same way using the processes of activation (p6, p7 and p8). Activated MPK-1 then moves from the cytoplasm to the nucleus. This movement is modeled as a translocation reaction by p9.
Based on the understanding of the literature and the hypothesis reported in [9], we first model downstream regulation of Ras/MAPK cascades and succedent intracellular reactions induced by LIN-12/Notch signaling according to newly published literature. The details of the new biological facts are described in the caption of Figure 4. The new facts concerning the mechanisms of the downstream regulation of Ras/MAPK cascades are modeled as follows: The phosphorylation by m12 further disrupts the formation of LIN-31/LIN-1 complex (m13) which applies the process of phosphorylation (p13). The processes p14 and p15 are used to model the transcription of target genes and the translation of mRNA (m16) regulated by LIN-31 (m31) that acts as a transcriptional activator promoting the 1° fate as a fate candidate (m18).
Two biological fate determination rules applied to VPC fate model
When determining cell fates from biological points of view, several biological fate determination rules can be taken into account. One major biological fate determination rule (Rule II) based on temporal order has been applied to a qualitative model by Fisher et al. [9]. The approach is based on a discrete model. However, the other rules such as temporal interval based one (Rule I) cannot be handled in the same discrete model. This is because the model cannot deal with the quantitative properties (e.g., continuous feature) that are also important to biological processes, such as the concentration of proteins and reaction rates. With inspiring by this limitation of qualitative models, we employ these two major biological fate determination rules – Rule I and Rule II – to VPC fate model. The model has both discrete and continuous features.
Two fate determination rules are as follows: (i) For Rule I, the fate will be determined if it satisfies the conditions that (1) the fate can sustain the behaviors at a certain over-threshold state within a given length of time, and (2) the time epoch of the certain over-threshold in (1) is earlier than the other fate candidate. Figure 7 shows a schematized diagram of a simulation result. In Figure 7, the cell fate is determined to the 2° fate by using Rule I. The time course expression of 1° is maintained at the over-threshold state during interval_ 1, and that of 2° is maintained at the over-threshold state during interval_ 2. Although the time course expression of 1° has two over-threshold states, only the second interval interval _1 is longer than the given interval. Thus, the time epoch labeled with "τ i of Rule I" is regarded as the initial time epoch inducing the second over-threshold state. The VPC adopts the 2° fate due to τ j <"τ i of Rule I".
A schematized diagram depicting the fate specification methods by using Rule I and Rule II. "τ i of Rule I" represents the first time epoch that the concentration of 1° (m18) exceeds threshold_ 1, and the time length interval_ starting from "τ i of Rule I" is longer than or equal to the given interval when using Rule I. "τ j of Rule II" represents the first time epoch that the concentration of 1° exceeds threshold_ 1, no matter how long this interval will continue when using Rule II. τ i represents the first time epoch that the concentration of 2° (m30) exceeds threshold_ 2. Variables m18 (denoting the concentration of 1°) and m30 (denoting the concentration of 1°) are regarded as two cell fate candidates for determining final VPC fate. Pn.p_fate 1/2_record 1/2 indicated in the brackets are the entity names used in Cell Illustrator.
-
(ii)
For Rule II, the cell fate will be priorly adopted according to the temporal sequence of the first time epoch inducing over-threshold state. In Figure 7, we can observe that the first time epoch (i.e., "τ i of Rule II") inducing over-threshold state of 1° is earlier than 2°, and therefore the 1° fate will be adopted by Rule II no matter how long the over-threshold state of 1° will continue. Preliminary notations and mathematical definitions of two rules are given in the Additional file 1.
In Figure 6, two dashed-line ellipses illustrate the topological connections representing Rule I (blue ellipse) and Rule II (red ellipse) which jointly use the values of m18 and m30 as the inputs for the fate specification. Variables m18 (denoting the concentration of 1°) and m30 (denoting the concentration of 2°) are regarded as two cell fate candidates for determining final VPC fate. Two rules are implemented with a script-based language Pnuts in Cell Illustrator [48]. The detailed properties and descriptions of the entities concerning the fate specification are summarized in Table 4. The activity functions of related processes and update functions of the connectors are summarized in Tables 5 and 6.
Further, several variables are designed to reserve alterable values according to different genotypes (see Table 7). Figure 8 shows a Genotype Configuration panel and a structure of auto-switching mechanism. The Genotype Configuration panel includes an AC and four mutant variables. AC, lin15, vul and lst can toggle between true and false. lin12 has three string-type values, i.e., "wt", "ko", "gf", indicating three genetic conditions of wild, knockout and overexpression of lin-12.
It is obvious that the combination number is 48 as listed in Table 8. Forty-eight genotypes have the features as follows:
-
(i)
For 15 genotypes whose RowID are indicated by boldface and labeled with square brackets, the fate patterns of each genotype have the in vivo experimental data reported in [32] (refer to the column of "Fate Patterns (ST)" in Tables 8 and 9).
-
(ii)
For eight genotypes whose RowID are indicated with the superscript (†), the fate patterns of each genotype have been confirmed by model checking approach in the discrete model in [9], which are also consistent with the biological facts [35, 46, 49–53].
-
(iii)
For the left 25 genotypes, the patterns of each genotype have only been verified in [9], because these genotypes are usually experimentally intractable. The reason is that, the population of double, triple or quadruple mutants might be technically difficult to be generated [9].
-
(iv)
For four genotypes (i.e., RowID 5, 21, 29, and 45) are called unstable patterns, because genetic condition will lead to an unstable fate pattern as shown in Table 9.
In the next subsection, we will execute simulation to investigate the characteristics of predicted fate patterns of 48 genotypes, in particular, four genotypes leading to the unstable fate pattern, and to evaluate two rules employed to the VPC fate model by comparing with three simulation targets (i.e., JA, ST, and STA) as shown in Figure 1(b).
Simulation-based model checking approach of determining VPC specification by using Cell Illustrator
We first demonstrate how to assign parameters to the VPC fate model. Then, we consider three simulation targets to investigate the properties of fate patterns, and to evaluate two proposed rules. Finally, a large number of simulations are performed with the use of "High-Speed Simulation Module" of Cell Illustrator. The simulation results are given in the form of fitting score and variation frequency of each pattern of 48 genotypes. The fitting score is a percentage of the total numbers of predicted patterns appeared in each genotype); the variation frequency is the number of each appearing fate pattern in the respective genotype during the simulation experiments.
Parameter assignment
The VPC fate model in Figure 5 reflects the interrelation of each substance. All parameters for the reaction rates of processes and the steady state of the substance are tuned manually with repeating simulation until concentration behaviors of proteins correspond to the biological facts. Note that it is hard to decide optimal values of these parameters, since data from biological experiments are very insufficient to determine them.
We thus simplify the kinetic parameters to the same speeds m
x
*0.1 with noise for the process p
i
∈ {p1, p2, ⋯, p24} (see Table 2); the speed of the source process  is assigned to 1.0 denoting the production rate of substance. When constructing the quantitative VPC fate model, threshold values (partly shown in Figure 8 and Table 10) of each reaction are assigned as real number, and the parameters for the steady states of the substances induced by the stimulations from anchor cell and hyp7 are carefully tuned by hand. Lots of trial and error operations have been performed repeatedly until appropriate parameters for simulation are determined. The VPC fate model in Figure 5 is available from [54], which can be executed on Cell Illustrator [24] or Java web start software Cell Illustrator Online 4.0 (CIO) [25]. All the parameters have been saved in the csv format, which are also available online at the same website [54].
is assigned to 1.0 denoting the production rate of substance. When constructing the quantitative VPC fate model, threshold values (partly shown in Figure 8 and Table 10) of each reaction are assigned as real number, and the parameters for the steady states of the substances induced by the stimulations from anchor cell and hyp7 are carefully tuned by hand. Lots of trial and error operations have been performed repeatedly until appropriate parameters for simulation are determined. The VPC fate model in Figure 5 is available from [54], which can be executed on Cell Illustrator [24] or Java web start software Cell Illustrator Online 4.0 (CIO) [25]. All the parameters have been saved in the csv format, which are also available online at the same website [54].
Three simulation targets for validation
[Obtaining fate patterns (JA) by using model checker: MOCHA]
Model checking is powerful technique for automatically verifying the system requirements. The essential idea of model checking is that, with an exhaustive exploring of all reachable states and transitions of a modeled system, system properties (expressed as a formal specification) are examined whether the properties are satisfied or not. A model checker (e.g., MOCHA[55]) accepts the modeled system and the specification as its inputs. The checker then outputs yes if the model satisfies the given specification and generates a counterexample otherwise. The counterexample indicates why the model does not satisfy the given specification. By repeating operations of revising the errors examined by the counterexamples, the modeled system can be refined to satisfy enough system specifications [1, 2].
Fisher et al. have firstly applied the model checking approach for validating biological systems of C. elegans with biological experiments [9]. They have constructed a discrete and state-based mechanistic model underlying the inductive and lateral signaling crosstalk by using the language of reactive modules [13] and MOCHA. Further, they have confirmed that the model can reproduce reported biological behavior observed in 22 genotypes with MOCHA. However, their method has the following weaknesses that are desired to be solved in this paper:
-
(1)
The details of predicted fate patterns of four unstable patterns (RowID 5, 21, 29, and 45) are not explicitly given. That is, only summarized patterns are given. However, it is important to reveal if all the expansions of predicted (summarized) patterns will appear even though the predicted patterns satisfy the given specification. For example, in the case of ac-; lin-12gf; lin-15ko double mutants (RowID 45 in Table 8), the predicted pattern is [1/2, 1/2, 1/2, 1/2, 1/2, 1/2 ] in [9]. It is obvious that the pattern includes totally 26 = 64 possible fate patterns, but it is still ambiguous if all these 64 patterns will be adopted in in vivo experiments.
-
(2)
The distribution and variation of individual behavior of predicted fate patterns are not sufficient to understand the features of the fate patterns. In other words, it is necessary to clarify the occurrence probability (called variation frequency) of each predicted pattern, which is considered to facilitate obtaining an overall distribution of the predicted fate patterns, especially, the four unstable patterns.
To improve the first weakness, we introduce a new procedure GENERATE NECESSARY FATE PATTERNS by repeating the use of "counterexample" to obtain necessary fate patterns on MOCHA.
«PROCEDURE GENERATE NECESSARY FATE PATTERNS»
[******]: A state pattern of six VPC fates; * is one of three alternative fates (1°, 2°, and 3°); i.e., [111111] denotes a fate pattern with 1° for all VPCs. In total, there are 729(= 36) fate patterns.
RS: A set to store intermediate fate patterns required for a genotype.
Verify: A MOCHA procedure to verify if the predication holds for the model. The input is the RS. If there is no counterexample for the RS, ϕ will be returned. If the counterexample is generated for the RS, one of the counterexamples will be returned at random.
The new procedure to derive whole fate patterns for a genotype is as follows:
-
1.
RS ? {[111111]}
-
2.
do c ? Verify(RS)
-
3.
RS ? RS ? {c}
-
4.
while c ? ?
-
5.
c ? Verify(RS\{[111111]})
-
6.
if c = ?
-
7.
return RS\{[111111]}
-
8.
else
-
9.
return RS
In the above procedure, step 1 is an initialization of RS. Steps 2 – 4 are the main part to obtain the fate patterns by repeating the use of "counterexample". Steps 5 – 9 are designed to check if the initial fate pattern is necessary or not. By executing the procedure, the results of required fate patterns of 48 genotypes are summarized in the fourth column of Table 8, and the first and fourth columns of Table 9. The predicted fate patterns of each genotype derived by using our procedure are collectively called Fate Patterns (JA) (JA for short). It is clear that the number of predicted fate patterns investigated by our method is far smaller than the one summarized by [9] (see Table 9). The source code used to obtain JA with MOCHA can be found at the CSML website [54].
[Fate patterns (ST) obtained from in vivo data]
Sternberg and Horvitz have summarized the VPC fate patterns of 15 genotypes by the observation of anatomy and the cell lineages in living C. elegans using Nomarski differential interference contrast optics (see Table 4 in the original paper [32]). We list the fate patterns of these 15 genotypes (refer to the fifth column in Table 8, and the second and fifth columns in Table 9).
[Fate patterns (STA) obtained from in vivo data including hybrid lineage observations]
In [32], we have noticed that some biological observations of cell lineages have not received enough attentions. These observations are likely difficult to be determined accurately according to the two criteria defined by Sternberg and Horvitz [32, 39]. The reason is that some lineages were not interpretable as 1° or 2° by two criteria, i.e., observed lineages may result in possible inaccuracy in the observations which includes mis-scoring adherence to ventral cuticle owing to deformations in cuticle as animals bend, as well as variations in division axes [32]. In some cases, lineages are hybrid, e.g., [S TT] in which [S] is the production of the characteristics of the 3° fate, and [TT] can be the lineage of either the 1° or 2° fate. Sternberg and Horvitz have suggested that hybrid sublineage is a result of imprecise decision, and the specification is allowed to have a number of outcomes. When a system comes close to a certain threshold, it can be considered that partial functions are involved to express the results in the formation of hybrid lineage [39].
Inspired by the observation of hybrid lineage, it seems reasonable to put those uninterpretable experimental data together with the fate patterns of [32] (i.e., ST) as the simulation targets for validation. By investigating the experimental results of the vulval cell lineage given in [32], we explain the cell fate of such an uninterpretable lineage as three plausible fate candidates: 1°, 2°, and 3° fates. Thus, the VPC fate pattern including the uninterpretable lineage is extended to three predicted fate patterns (see STA block in Figure 1(b)). For example, in the case of vulko (RowID 3 in Table 8), we observed such a cell lineage: [[S S] [S S] [S S] [S TT] [S S] [S S] ], in which [S S] is a cell lineage of 3° and [S TT] is a hybrid lineage and is interpretable by neither two criteria defined in [32] nor the method in [9]. This cell lineage is determined by the fate pattern [333?33]. We thus suppose to interpret this VPC fate pattern to three fate pattern extensions of [3331 33], [3332 33], and [3333 33], i.e., extend "?" (uncertain fate) to the 1°, 2°, and 3° fate. All the possible cell fate patterns including extended fate patterns are shown in the column Fate Patterns (STA) of Tables 8 and 9, i.e., STA is the combination of ST and the pattern extensions.
Simulation procedures
Here, we discuss several considerations of simulation environment adjustment in order to validate the VPC fate model and evaluate two rules.
When emulating cell stimulations in in silico experiments, it is important to adjust the cell to a constant condition before the stimulation. This condition is usually called a steady state. For example, simulation time periods of 400 [pt] and 200 [pt] are reserved representing LIN-3 stimulations from AC and hyp7 respectively in the VPC fate model ([pt] is the virtual time unit of the HFPNe model). This is because the concentration of the receptor LET-23 will be kept at a steady state after 200 [pt]. The time interval of the stimulations between AC and hyp7 is designed to investigate respective variation of fate patterns.
Meanwhile, the following is taken into account to emulate real environment as well as assessing the robustness of the model:
-
(i)
The notion of log-normal distribution is introduced. For each process, log-normal distribution is applied as a system noise. Each standard deviation is given in the third column in Table 2, where LSMass(arg 1, arg 2) denotes the function of log-normal distribution, arg 1 denotes normal reaction speed without noise, and arg 2 is the standard deviation denoting the strength of the noise.
-
(ii)
In the case of lin-15ko mutant, a little temporal difference between the stimulations of LIN-3 emanating from hyp7 to each Pn.p is designed to investigate the influence of ectopic stimuli.
-
(iii)
The key thresholds involved in Ras/MAPK and LIN-12/Notch signaling pathways are assigned to the variables, which depend on the function of rand() that fluctuates randomly between 0.0 and 1.0 (refer to Table 10). Here, uniform random number generated by Mersenne Twister random number generator is used.
We have tried 100, 1,000 and 10,000-run simulation experiments. For all cases, the results clearly show that Rule I can generate high fitting score than Rule II. Among them, since 10,000-run simulation can present the most precise behaviors of each fate pattern, in this paper we have concentrated on the 10,000-run simulation results to investigate the fitting score and variation frequency of 48 genotypes on the VPC fate model. The simulation experiments are carried out on the workstation of Intel Xeon X5450 (3.0 GHz) processors with 16 Gbytes of memory. The machine has two CPUs which has four cores per CPU (number of total processor cores is eight). The theoretical computational performance is 96 GFLOPS. All simulations were run on Java 1.6 environment. The VPC fate model will take nearly 100 [sec] for one simulation on Cell Illustrator with a script-based simulation engine. It provides detailed visualization of system behaviors. On the other hand, Cell Illustrator is equipped with a "High-Speed Simulation Module" specialized in producing simulation results only. It increases the simulation speed from 10 to 100 times than the script-based one. Hence, the 10,000 simulations can be conducted on a day on average, and the 48 sets can be executed on 48 days on a single core of a processor. We carried out all simulations within 6 days on our computing environment. We use the same model, the same procedures and also the same parameters to evaluate the fate patterns of all 48 genotypes with the three simulation targets (refer to Tables 8 and 9).
Results and Discussion
We now exhibit and discuss our simulation results on the fitting score of predicted fate patterns and the variation frequency of each appearing fate pattern, especially focusing on the four unstable patterns.
Using the method addressed in the previous sections, we performed the simulation of the VPC fate model. Tables 10, 11, 12, 13, 14 and Additional file 2 exhibit the simulation results of 48 genotypes. Figures 9, 10, 11 and 12 show the graphs of four unstable patterns (RowID 5, 21, 29, and 45), which depict the variation frequency of each predicted pattern and the variation distribution based on simulation results. For example, in Figure 9, the fate pattern [122121] predominantly appeared in the matched results of JA by using Rule I and Rule II, while the pattern is regarded as a false pattern because it is not observed in ST and STA.
From the variation distribution as shown in Figure 9, [122121] is the fate pattern that can be most easily observed in in vivo experiments because of the high appearance. In contrast, [112121] is likely difficult to be monitored due to the relative low variation frequency. Each graph comprises three parts of comparison results obtained from JA, ST and STA (see (a), (b), and (c) in Figure 9) by using both Rule I and Rule II. In each part, the variation frequency results of matched patterns are given on the left side while that of unmatched patterns are exhibited on the right side. Figures 10, 11 and 12 are built up in the same way.
From the simulation results, we draw the following conclusions:
-
(1)
Rule I gives more genotypes (RowID) with high fitting scores nearly 100% than Rule II to cover predicted patterns of three simulation targets. In more details,
-
(i)
For 44 genotypes (i.e., the genotypes without unstable fate patterns), each genotype can generate the fitting score nearly 95%, in which the fitting scores of 41 genotypes are all 100% (refer to Additional File 1) by using both Rule I and Rule II. In other words, our model shows good robustness, and can produce stable cell fate patterns even we intentionally add the noise to capture the behaviors of the model fluctuations.
-
(ii)
For the left three genotypes of four unstable fate patterns, lin-15ko mutant (RowID 5) produces all 92.6% for JA, ST and STA by using Rule I, as opposed to 24.4% (for JA) and 36.96% (for ST and STA) by using Rule II; ac-; lin-15ko mutant (RowID 29) produces high coverage of 94.11% (for JA) and 99.86% (for both ST and STA); and ac-; lin-12gf; lin-15ko double mutants (RowID 45) generates all 100% with both rules for three simulation targets.
-
(iii)
For lin-15; lin-12ko double mutants (RowID 21), the fitting scores in the results of ST and STA drop to a quite low value below 15% by using either Rule I or Rule II. This is because P3.p is allowed to adopt the 1° fate in JA (in silico model), but is not allowed in ST and STA (in vivo model). This fact has also been confirmed in the preceding study [9] that in silico model can faithfully produce the 1° fate for P3.p. From these observations, it can be considered that P3.p has a greater possibility to adopt the 1° fate, if the number of animals for the in vivo experiments can be increased to 10,000. In this way, the fitting score can be exactly increased to exceed more than 81% from the present 15%.
-
(i)
-
(2)
For lin-15ko (RowID 5) and ac-;lin-15ko (RowID 29) genotypes, we can see that nearly 10% patterns in JA, ST and STA are not matched (refer to Tables 11 and 13). These patterns still have the possibility to be examined in in vivo experiments by means of enlarging animal population.
-
(3)
Since the experiment data about hybrid lineages has not been taken into account as we have pointed out, we interpret these uninterpretable lineages to three fate pattern extensions as listed in the column of STA which includes more extensive possible fate patterns than ST. In the simulation results, the results of lin-12ko mutant (RowID 9) interest us (refer to the Additional file 1). We can find that the fate pattern [331133] appeared in our simulation results of STA, which is the extended fate pattern from the hybrid lineage data exhibited in [32]. This hybrid lineage gives new insights on the imprecise fate decision and the fate specification mechanisms when a system comes close to a certain threshold.
Taking these observations together, we conclude that Rule I relying on the temporal interval can be considered more reasonable and proper in evaluating the VPC fate specification than Rule II.
Conclusion
The contribution of this paper is a novel method of modeling and simulating biological systems with the use of model checking approach on the hybrid functional Petri net with extension. A quantitative HFPNe model for the vulval development is constructed based on the literature. Then we employ two major biological fate determination rules to the quantitative model. These two rules are investigated by applying model checking approach in a quantitative manner. Three simulation targets of this model are considered: The first one is the fate patterns obtained by improving the qualitative method of Fisher et al. [9]; the second target is the fate patterns summarized by Sternberg and Horvitz [32]; and the last one is derived from the biological experiments in [32] including the hybrid lineage data. We have performed 480,000 simulations on the quantitative HFPNe model by using Cell Illustrator. We have examined the consistency and the correctness of the model, and evaluated the two rules of VPC fate specification. We consider that this computational experiment and the biological evaluation could not be easily put into practice without the HFPNe modeling method and the functions of Cell Illustrator, especially, the "High-Speed Simulation Module". Finally, in silico simulation results have been given in the form of the fitting score and the variation frequency of each pattern. We have discussed the results and summarized several plausible explanations.
Abbreviations
- AC:
-
(gonadal anchor cell)
- ac-:
-
(absence of an anchor cell)
- EGFR:
-
(the epidermal growth factor receptor)
- HFPNe:
-
(hybrid functional Petri net with extension)
- JA:
-
(fate patterns obtained with our extended method from the discrete model of Fisher et al. [9])
- LBS:
-
(LAG-1 binding site)
- lst:
-
(lateral signal target)
- MAPK:
-
(mitogen-activated protein kinases)
- ST:
-
(fate patterns summarized by Sternberg and Horvitz [32])
- STA:
-
(fate pattern combinations consisting of ST and the pattern extensions)
- VPC:
-
(vulval precursor cell)
- synMuv:
-
(synthetic Multivulva)
References
Clarke EM, Grumberg O, Peled DA: Model Checking. 1999, The MIT Press
Bérard B, Bidoit M, Finkel A, Laroussinie F, Petit A, Petrucci L, Schnoebelen P, McKenzie P: Systems and Software Verification: Model-Checking Techniques and Tools. 2001, Springer
Clarke EM, Emerson EA: Design and synthesis of synchronization skeletons using branching time temporal logic. Logic of Programs. 1982, 52-71. New York: Springer Berlin/Heidelberg
Queille JP, Sifakis J: Specification and verification of concurrent systems in CESAR. Lecture Notes in Computer Science. 1982, 137: 337-351.
Chabrier N, Fages F: Symbolic model checking of biochemical networks. Proceedings of CMSB 2003 (Computational Methods in Systems Biology). 2003, 149-162. Italy: Springer Berlin/Heidelberg
Antoniotti M, Policriti A, Ugel N, Mishra B: Model building and model checking for biochemical processes. Cell Biochem Biophys. 2003, 38 (3): 271-286.
Batt G, Ropers D, de Jong H, Geiselmann J, Mateescu R, Page M, Schneider D: Validation of qualitative models of genetic regulatory networks by model checking: analysis of the nutritional stress response in Escherichia coli. Bioinformatics. 2005, 21 (Suppl 1): i19-i28.
Calder M, Vyshemirsky V, Gilbert D, Orton R: Analysis of signalling pathways using the prism model checker. Proceedings of CMSB 2005 (Computational Methods in Systems Biology). Edited by: Plotkin G. 2005, 179-190. University of Edinburgh
Fisher J, Piterman N, Hajnal A, Henzinger TA: Predictive modeling of signaling crosstalk during C. elegans vulval development. PLoS Comput Biol. 2007, 3 (5): e92-
Heath J, Kwiatkowska M, Norman G, Parker D, Tymchyshyn O: Probabilistic model checking of complex biological pathways. Theor Comput Sci. 2008, 391 (3): 239-257.
Kwiatkowska MZ, Norman G, Parker D: Using probabilistic model checking in systems biology. SIGMETRICS Performance Evaluation Review. 2008, 35 (4): 14-21.
Monteiro PT, Ropers D, Mateescu R, Freitas AT, de Jong H: Temporal logic patterns for querying dynamic models of cellular interaction networks. Bioinformatics. 2008, 24 (16): i227-i233.
Alur R, Henzinger TA: Reactive modules. Formal Methods in System Design. 1999, 15: 7-48.
Regev A, Silverman W, Shapiro E: Representation and simulation of biochemical processes using the pi-calculus process algebra. Pac Symp Biocomput. 2001, 459-470.
Hatakeyama M, Kimura S, Naka T, Kawasaki T, Yumoto N, Ichikawa M, Kim JH, Saito K, Saeki M, Shirouzu M, Yokoyama S, Konagaya A: A computational model on the modulation of mitogen-activated protein kinase (MAPK) and Akt pathways in heregulin-induced ErbB signalling. Biochem J. 2003, 373 (2): 451-463.
Matsuno H, Tanaka Y, Aoshima H, Doi A, Matsui M, Miyano S: Biopathways representation and simulation on hybrid functional Petri net. In Silico Biol. 2003, 3 (3): 389-404.
Nagasaki M, Doi A, Matsuno H, Miyano S: Computational modeling of biological processes with Petri net based architecture. Bioinformatics Technologies. Edited by: Chen YP. 2005, Springer Berlin Heidelberg
Nagasaki M, Doi A, Matsuno H, Miyano S: A versatile Petri net based architecture for modeling and simulation of complex biological processes. Genome Inform. 2004, 15 (1): 180-197.
Pinney JW, Westhead DR, McConkey GA: Petri net representations in systems biology. Biochem Soc Trans. 2003, 31 (Pt 6): 1513-1515.
Matsuno H, Li C, Miyano S: Petri net based descriptions for systematic understanding of biological pathways. IEICE Trans Fundamentals. 2006, E89-A (11): 3166-3174.
Li C, Ge QW, Nakata M, Matsuno H, Miyano S: Modelling and simulation of signal transductions in an apoptosis pathway by using timed Petri nets. J Biosci. 2007, 32 (1): 113-127.
Chaouiya C: Petri net modelling of biological networks. Brief Bioinform. 2007, 8 (4): 210-219.
Koch I, Heiner M: Petri nets. Analysis of Biological Networks. Edited by: Junker BH, Schreiber F. 2008, 139-180. A Wiley Interscience Publication
Cell Illustrator. http://www.cellillustrator.com/
Cell Illustrator Online. , http://cionline.hgc.jp/
Nagasaki M, Doi A, Matsuno H, Miyano S: Genomic Object Net: I. A platform for modelling and simulating biopathways. Appl Bioinformatics. 2003, 2 (3): 181-184.
Doi A, Fujita S, Matsuno H, Nagasaki M, Miyano S: Constructing biological pathway models with hybrid functional Petri nets. In Silico Biol. 2004, 4 (3): 271-291.
Doi A, Nagasaki M, Fujita S, Matsuno H, Miyano S: Abstract Genomic Object Net: II. modelling biopathways by hybrid functional Petri net with extension. Appl Bioinformatics. 2003, 2 (3): 185-188.
Matsuno H, Doi A, Nagasaki M, Miyano S: Hybrid Petri net representation of gene regulatory network. Pac Symp Biocomput. 2000, 341-352.
Matsuno H, Murakami R, Yamane R, Yamasaki N, Fujita S, Yoshimori H, Miyano S: Boundary formation by notch signaling in Drosophila multicellular systems: experimental observations and gene network modeling by Genomic Object Net. Pac Symp Biocomput. 2003, 152-163.
Troncale S, Tahi F, Campard D, Vannier JP, Guespin J: Modeling and simulation with hybrid functional Petri nets of the role of interleukin-6 in human early haematopoiesis. Pac Symp Biocomput. 2006, 427-438.
Sternberg PW, Horvitz HR: The combined action of two intercellular signaling pathways specifies three cell fates during vulval induction in C. elegans. Cell. 1989, 58 (4): 679-693.
Peterson JL: Petri Net Theory and the Modeling of Systems. 1981, Prentice Hall
Greenwald I: LIN-12/Notch signaling in C. elegans. Worm Book. 2005, 8: 1-16.
Yoo A, Bais C, Greenwald I: Crosstalk between the EGFR and LIN-12/Notch pathways in C. elegans vulval development. Science. 2004, 303 (5658): 663-666.
Christensen S, Kodoyianni V, Bosenberg M, Friedman L, Kimble J: lag-1, a gene required for lin-12 and glp-1 signaling in Caenorhabditis elegans, is homologous to human CBF1 and Drosophila Su(H). Development. 1996, 122 (5): 1373-1383.
Cui M, Chen J, Myers TR, Hwang BJ, Sternberg PW, Greenwald I, Han M: SynMuv genes redundantly inhibit lin-3/EGF expression to prevent inappropriate vulval induction in C. elegans. Dev Cell. 2006, 10 (5): 667-672.
Miller LM, Gallegos ME, Morisseau B, Kim S: lin-31, a Caenorhabditis elegans HNF-3/fork head transcription factor homolog, specifies three alternative cell fates in vulval development. Genes Dev. 1993, 7 (6): 933-947.
Sternberg PW, Horvitz HR: Pattern formation during vulval development in C. elegans. Cell. 1986, 44 (5): 761-772.
Lackner M, Kornfeld K, Miller LM, Horvitz HR, Kim S: A MAP kinase homolog, mpk-1, is involved in ras-mediated induction of vulval cell fates in Caenorhabditis elegans. Genes Dev. 1994, 8 (2): 160-173.
Shaye DD, Greenwald I: Endocytosis-mediated downregulation of LIN-12/Notch upon Ras activation in Caenorhabditis elegans. Nature. 2002, 420 (6916): 686-690.
Sternberg PW: Vulval development. Worm Book. 2005, 25: 1-28.
Kohara Y: Caenorhabditis elegans – Symphony of 1000 Cells. 1997, In Japanese, Kyoritsu Shuppan
Riddle DL, Blumenthal T, Meyer BJ, Priess JR: C. Elegans II: Monograph 33. 1998, Cold Spring Harbor Laboratory Press
Tan PB, Lackner MR, Kim SK: MAP kinase signaling specificity mediated by the LIN-1 Ets/LIN-31 WH transcription factor complex during C. elegans vulval induction. Cell. 1998, 93 (4): 569-580.
Berset T, Hoier EF, Battu G, Canevascini S, Hajnal A: Notch inhibition of RAS signaling through MAP kinase phosphatase LIP-1 during C. elegans vulval development. Science. 2001, 291 (5506): 1055-1058.
Jeong E, Nagasaki M, Saito A, Miyano S: Cell System Ontology: Representation for modeling, visualizing, and simulating biological pathways. In Silico Biol. 2007, 7 (6): 623-638.
Pnuts., http://www.pnuts.org/
Sulston JE, Horvitz HR: Post-embryonic cell lineages of the nematode, Caenorhabditis elegans. Dev Biol. 1977, 56 (1): 110-156.
Berset TA, Hoier EF, Hajnal A: The C. elegans homolog of the mammalian tumor suppressor Dep-1/Scc1 inhibits EGFR signaling to regulate binary cell fate decisions. Genes Dev. 2005, 19 (11): 1328-1340.
Ferguson EL, Sternberg PW, Horvitz HR: A genetic pathway for the specification of the vulval cell lineages of Caenorhabditis elegans. Nature. 1987, 326 (6110): 259-267.
Kimble J: Alterations in cell lineage following laser ablation of cells in the somatic gonad of Caenorhabditis elegans. Dev Biol. 1981, 87 (2): 286-300.
Han M, Aroian RV, Sternberg PW: The let-60 locus controls the switch between vulval and nonvulval cell fates in Caenorhabditis elegans. Genetics. 1990, 126 (4): 899-913.
VPC fate specification of C. elegans in CSML., http://www.csml.org/models/csml-models/vulvaldev/
Alur R, Henzinger TA, Mang FYC, Qadeer S, Rajamani SK, Tasiran S: MOCHA: modularity in model checking. Lecture Notes in Computer Science. 1998, 1427: 521-525.
Acknowledgements
We are grateful to the anonymous reviewers for their valuable hints and suggestions. This work was supported by KAKENHI (Grant-in-Aid for Scientific Research) on Priority Areas "Systems Genomics" from the Ministry of Education, Culture, Sports, Science and Technology of Japan.
Author information
Authors and Affiliations
Corresponding author
Additional information
Authors' contributions
The basic idea was considered by MN and further developed by CL and MN. CL created biological diagram of multiple signaling pathways of C. elegans depicting VPC fate specification in Figure 4. CL and KU constructed the original HFPNe model in Figures 5 and 6. The whole HFPNe model was refined by CL and MN. CL and MN evaluated the results of simulation and validated the performance of HFPNe model. SM supervised the whole study. The final manuscript was read and approved by all authors.
Chen Li, Masao Nagasaki contributed equally to this work.
Electronic supplementary material
12918_2008_310_MOESM1_ESM.pdf
Additional File 1: Preliminary notations and mathematical definitions of Rule I and Rule II. The data provide the details of preliminary notations and mathematical definitions of two rules to determine the cell fate. (PDF 40 KB)
12918_2008_310_MOESM2_ESM.pdf
Additional File 2: Simulation results of 44 genotypes. The data give the 10,000 simulation results without unstable fate patterns. Yellowish region means that corresponding genotype possesses experimental evidences exhibited in [32]. Bright yellow cells give the fitting scores of predicted fate patterns. (PDF 309 KB)
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
Open Access This article is published under license to BioMed Central Ltd. This is an Open Access article is distributed under the terms of the Creative Commons Attribution License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Li, C., Nagasaki, M., Ueno, K. et al. Simulation-based model checking approach to cell fate specification during Caenorhabditis elegans vulval development by hybrid functional Petri net with extension. BMC Syst Biol 3, 42 (2009). https://doi.org/10.1186/1752-0509-3-42
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1752-0509-3-42


 = {f |f :
= {f |f :  = {f |f :
= {f |f :  = {f |f :
= {f |f :  = {f |f :
= {f |f : 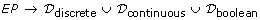 is a function called the activity function such that for a connector c
is a function called the activity function such that for a connector c 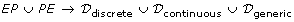 is a function called the update function which satisfies the following conditions: For a connector c
is a function called the update function which satisfies the following conditions: For a connector c 









