- Research article
- Open access
- Published:
Time-dependent structural transformation analysis to high-level Petri net model with active state transition diagram
BMC Systems Biology volume 4, Article number: 39 (2010)
Abstract
Background
With an accumulation of in silico data obtained by simulating large-scale biological networks, a new interest of research is emerging for elucidating how living organism functions over time in cells.
Investigating the dynamic features of current computational models promises a deeper understanding of complex cellular processes. This leads us to develop a method that utilizes structural properties of the model over all simulation time steps. Further, user-friendly overviews of dynamic behaviors can be considered to provide a great help in understanding the variations of system mechanisms.
Results
We propose a novel method for constructing and analyzing a so-called active state transition diagram (ASTD) by using time-course simulation data of a high-level Petri net. Our method includes two new algorithms. The first algorithm extracts a series of subnets (called temporal subnets) reflecting biological components contributing to the dynamics, while retaining positive mathematical qualities. The second one creates an ASTD composed of unique temporal subnets. ASTD provides users with concise information allowing them to grasp and trace how a key regulatory subnet and/or a network changes with time. The applicability of our method is demonstrated by the analysis of the underlying model for circadian rhythms in Drosophila.
Conclusions
Building ASTD is a useful means to convert a hybrid model dealing with discrete, continuous and more complicated events to finite time-dependent states. Based on ASTD, various analytical approaches can be applied to obtain new insights into not only systematic mechanisms but also dynamics.
Background
A great deal of biological datasets have been measured in a lot of laboratories around the world in recent years. Petri nets have been applied successfully in modeling, simulating and analyzing biological networks [1, 2] (i.e., metabolic [3, 4], signal transduction [5, 6] and gene regulatory networks [7, 8]). In the meanwhile, a number of public and commercial databases have developed tools to automatically convert biological pathway information into various formats of models, e.g., the tool TRANSPATH2CSML [9] automatically converts data stored in TRANSPATH [10] to a simulation-based model encoded in a biological pathway format. These approaches make it possible to construct larger and more complex biological network models. However, the associated increase in complexity and output data result in the difficulty of grasping systematic characteristics of the models.
Several studies with respect to the topology of the interactions between biological compounds in cellular networks based on Petri net theory have been made in understanding biological networks [11–14]. These approaches use mathematical properties of Petri nets (e.g., reachability, liveness, boundedness and T-invariant) to reveal some topological properties of biological networks on qualitative models. Other investigation regarding the dynamics of signal propagation in signaling pathway has been given by Hardy et al.[15]. This method gives temporal information about the flow of signal propagation. However, the analysis is limited to a single signal source. Nevertheless, it is expected to find a general methodology to analyze the dynamics with quantitative simulation information, i.e., time-dependent dynamic behaviors among genes and their products which constitute biological networks [16].
This paper presents a novel method to build a framework for automatically constructing a so-called active state transition diagram (ASTD) for the dynamic analysis with respect to the structural changes over time in a hybrid functional Petri net with extension (HFPNe) model. Our method incorporates time-course simulation data and temporal structural properties (connection relationship) of the HFPNe model. This method constructs an ASTD composed of unique temporal subnets which are exhaustively extracted from original HFPNe model, produces a simplified graphical representation about the temporal information of the dynamics. After the ASTD is built, various analysis can be applied to the ASTD to obtain new insights into the systematic dynamics. Note that HFPNe is an enhanced Petri net architecture which involves the functions of existing high-level Petri nets [17].
The paper is organized as follows. In Methods, we first present a basic definition of HFPNe. We propose two new algorithms for constructing ASTD based on time-course simulation data from an HFPNe model. In Results and Discussion, we present a case study describing how our method is employed to integrate and interpret the circadian rhythm model in Drosophila, and give three characteristic overviews of the ASTD for facilitating a system-level understanding. The final section concludes our paper and addresses the contribution.
Methods
Hybrid functional Petri net with extension (HFPNe)
Hybrid functional Petri net with extension (HFPNe) is a mathematical tool for modeling and simulating biological networks. HFPNe can deal with three types of data - discrete, continuous and generic - and is comprised of three types of elements - places, transitions and arcs - whose symbols are illustrated in Figure 1.
A discrete place holds a positive integer number of content. A discrete transition is the same notion as used in the traditional discrete Petri net [18]. A continuous place holds a nonnegative real number as concentration of a substance such as mRNA and protein. A continuous transition is used to represent a biological reaction such as transcription and translation, at which the reaction speed is assigned as a parameter. A generic place can hold any kind of types including object, e.g., the string of nucleotide base sequence. A generic transition can deal with any kind of operations (e.g., alternative splicing and frameshifting) to all types of places. Generic place and transition have been practically applied for modeling and simulating more complicated biological processes [7, 19, 20], e.g., activities of enzymes for a multi-modification protein. Arcs are classified into three types: normal arc, test arc, and inhibitory arc. Normal arc connects a place to a transition or vice versa. Test or inhibitory arc represents a condition and is only directed from a place to a transition. Each of normal arc from a place, test arc, and inhibitory arc has a threshold by which the parameter assigned to the transition at its head is controlled. A normal arc from a place or a test arc (an inhibitory arc) can participate in activating (repressing) a transition at its head, as far as the content of a place at its tail is over the threshold. For either of test or inhibitory arcs, no amount is consumed from a place at its tail.
Basic definitions for HFPNe
We briefly give the necessary definitions for HFPNe used in this paper. The formal definition of HFPNe is given as additional material [see Additional file 1]. For further definition and application of HFPNe the reader is suggested to refer to Nagasaki et al.[17]. The following is the mathematic definitions used in this paper:
Definition 1. A hybrid functional Petri net with extension (HFPNe) H = (P, T, A, τ, w, u, d) consists of the following:
-
1.
P is a set of places and T is a set of transitions. Place is labeled with either discrete, continuous, or generic. Transition is also labeled with discrete, continuous, or generic. The place and transition are called discrete, continuous, or generic according to its label.
For each transition t in T, it has two sets Input t and Output t of arcs. Arc a∈Input t is an edge from input place p a to the transition t called input arc. Arc a'∈Output t is an edge from the transition t to output place p a' called output arc. Each arc is labeled with either normal, test, or inhibitory, and arc labeled with normal (resp., test, inhibitory) is called normal arc (resp., test arc, inhibitory arc). We also say that arcs (a and a') are discrete (resp., continuous, generic) if transition t is discrete (resp., continuous, generic).
We denote by PT and TP the set of input arcs and the set of output arcs of all transitions, respectively. We also denote arc a in PT as a(p, t). In a similar way, arc a' in TP is denoted as a'(t, p). The set A of arcs is given by PT∪TP.
-
2.
The types of places are given by a type function τ.
-
3.
For each input arc a∈PT, its activity w(a) is given by an activity function w. Activity function w(a) is used as a function giving the threshold in discrete and continuous cases and the condition in generic case, which is required for enabling the transition t.
-
4.
For each arc c (c = a(p, t)∈PT or c = a'(t, p)∈TP), the update u(c) is given by an update function u.
-
5.
For each discrete or generic transition t, the delay of t is given by a delay function d.
We use the parameter x ≥ 0 for the time in HFPNe. Do not confuse t for transition with x for time.
A marking of P is defined as a mapping M that assigns a mark (the type of contents) to each place. M [p] is called the mark of p. The initial marking I is a marking at time x = 0 and we denote the marking at time x by M(x). The reserved marking M
r
(x) at time x represents the amount of "tokens" reserved for firing when firing conditions are satisfied. By convention, let M(p, x) be M [p](x), and M
r
(p, x) be M
r
[p](x) for p∈P. We define 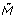 (x) by
(x) by 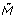 [p](x) = M [p](x)-M
r
[p](x) if p is discrete or continuous and
[p](x) = M [p](x)-M
r
[p](x) if p is discrete or continuous and 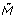 [p](x) = M [p](x) if p is generic. Given the initial marking of HFPNe, the marking M(x) and the reserved marking M
r
(x) at time x are defined in the following way:
[p](x) = M [p](x) if p is generic. Given the initial marking of HFPNe, the marking M(x) and the reserved marking M
r
(x) at time x are defined in the following way:
For time x = 0, M(0) = I by definition. We define M r [p](0) = 0 if p is discrete or continuous, and M r [p](0) = null (the empty list) if p is generic. For x> 0, we define M (x) and M r (x) in the following way. For transition t at time x, we say that t is enabled at time x if the following conditions are satisfied. Otherwise the transition is said to be disabled at time x.
-
1.
If t is discrete or continuous, then for all input arcs c = a(p, t)∈PT the following conditions hold:
-
(a)
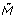 [p](x)>w(c) [M(x)] if a is not labeled with inhibitory;
[p](x)>w(c) [M(x)] if a is not labeled with inhibitory; -
(b)
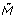 [p](x)<w(c) [M(x)] if a is labeled with inhibitory,
[p](x)<w(c) [M(x)] if a is labeled with inhibitory,
where w(c) [M(x)] is the threshold value of c on marking M at time x.
-
(a)
-
2.
If t is generic, then for all input arcs a(p, t)∈PT the following conditions hold:
-
(a)
w(a) [
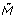 (x)] = true if a is not labeled with inhibitory;
(x)] = true if a is not labeled with inhibitory; -
(b)
w(a) [
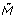 (x)] = false if a is labeled with inhibitory. □
(x)] = false if a is labeled with inhibitory. □
-
(a)
Definition 2. For arc c = a(p, t)∈PT at time x, we say that c is enabled at time x if the following conditions are satisfied. Otherwise, the arc c is said to be disabled at time x.
-
1.
If c is discrete or continuous, then
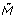 [p](x)>w(c) [M(x)] holds;
[p](x)>w(c) [M(x)] holds; -
2.
If c is generic, then w(c) [
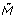 (x)] = true holds. □
(x)] = true holds. □
Definition 3. If disabled transition t turns enabled at time x, we say that t is triggered at time x and x is called the trigger time. If enabled transition t turns disabled at time x, we say that t is switched off at time x and x is called the switch-off time. □
Definition 4. We define firing of discrete transition t. Assume that discrete transition t is triggered at time x. For each normal input arc a(p, t), the place p must be discrete or continuous by definition. Then M r [p] reserves a · u(a) [M (x)], i.e., α·u(a) [M (x)] is added to M r [p], for the time y > x until x + d(t) [M(x)], where α = {0, 1}, if α = 0, reserve is disabled; otherwise, token is reserved. If t is still enabled at x + d(t) [M(x)], then at the same time x + d(t) [M(x)], M [p] is decreased by u(a) [M(x)] and M r [p] releases u(a) [M (x)], i.e., u(a) [M (x)] is decreased from M r [p]. Simultaneously, for each output normal arc a'(t, p'), M [p'] is increased by u(a') [M(x)] at time x + d(t) [M(x)] by arc a'(t, p'). The time d(t) [M(x)] is called the delay that is determined by the function d(t) of the mark M(x) at time x.
As we will describe in Definitions 5 and 6 below, the reservation is not performed by generic or continuous transition. However, for the place p, there may be another discrete transitions t1,..., tℓ with normal input arcs a1(p, t1),..., a
m
(p, tℓ) which are triggered at time x. Then each discrete transition t
i
tries to reserve u(a
i
) [M (x)] from the same M [p] at time x for i = 0,..., ℓ, where a0 = a(p, t) and t0 = t. We say that there is a conflict with p at time x if  . When a conflict occurs, some conflict resolution should be applied, e.g., random selection of transitions, priorities on transitions, etc.
. When a conflict occurs, some conflict resolution should be applied, e.g., random selection of transitions, priorities on transitions, etc.
Even if some conflict resolution procedure selected the transition t to go further, the place p of a(p, t) may be input places or output places of another discrete/continuous/generic transitions. By this, M [p] and M
r
[p], and therefore 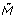 [p], may be changed, the conditions of "enabled" are not be necessarily satisfied until the firing time x + d(t) [M(x)]. When t becomes disabled before x + d(t) [M(x)], we say that a system error occurs with t.
[p], may be changed, the conditions of "enabled" are not be necessarily satisfied until the firing time x + d(t) [M(x)]. When t becomes disabled before x + d(t) [M(x)], we say that a system error occurs with t.
Thus triggered transition does not necessarily fire. If all of these actions succeed, we say that t fires at time x + d(t) [M(x)]. □
Note that α is set to zero in this paper so that the reserved marking M r (x) at any time x equals to zero. That is, the token amount will not be reserved during the delay time of the transition t when it becomes enabled.
Definition 5. We define firing of generic transition t. Assume that generic transition t is triggered at time x. For each normal input arc a(p, t), the place p can be discrete, continuous and generic. For each output normal arc a'(t, p'), p' can be also any kind of places. If t keeps enabled until time x + d(t) [M(x)], then M [p] at time x + d(t) [M(x)] is updated to u(a) [M(x)] and M [p'] is updated to u(a') [M(x)] at time x + d(t) [M(x)]. We say that t fires at time x + d(t) [M(x)] if this action succeeds. If p is generic, it is always that M
r
[p](x) = null. No change is added to M
r
[p] by arc a(p, t) if p is discrete or continuous. In a similar way to discrete transition, if p is discrete or continuous, Mp and M
r
[p] have a possibility to be changed before x + d(t) [M(x)] by another transitions. Therefore w(a)[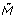 (y)] = true is not necessarily kept for y ∈ (x, x + d(t) [M(x)]). As in the case of discrete transition, it should be reported as system error. Since generic transition updates M [p] and M [p'] at time x + d(t) [M(x)], there is a possibility of conflict with another transitions which use p and p'. Thus some conflict resolution should be applied or it should be reported as system error. □
(y)] = true is not necessarily kept for y ∈ (x, x + d(t) [M(x)]). As in the case of discrete transition, it should be reported as system error. Since generic transition updates M [p] and M [p'] at time x + d(t) [M(x)], there is a possibility of conflict with another transitions which use p and p'. Thus some conflict resolution should be applied or it should be reported as system error. □
Definition 6. We define firing of continuous transition t. When continuous transition t is triggered, it starts firing and updates the marks of its connected places continuously with the speeds determined by the update function u and the marking M as long as it is enabled. Assume that continuous transition t is enabled at time x. For each normal input arc a(p, t), the place p must be continuous by definition. Then the mark M [p] will be decreased through the arc a(p, t) with the additional speed u(a) [M(x)] at time x. No change is added to M r [p] by arc a(p, t). For output normal arc a'(t, p'), the place p' must be continuous by definition. Then the mark M [p'] will be increased through the arc a'(t, p') with the additional speed u(a') [M(x)] at time x. No change is added to M r [p'] by arc a'(t, p'). □
HFPNe modeling
-
Places are used to model biological molecules, conditions, states and cellular organelles. In the case of chemical reactions, the compounds involved usually have specific quantities. In HFPNe, places can take any object that can be expressed in programming languages like an instance of a class in C++ or Java.
-
Transitions are used to model interactions among places, such as phosphorylation, translocation, and apoptosis. In HFPNe, each transition can define any event/function that can be performed by programming languages. In a simple model, the event/function can be the speed of a reaction or a discrete reaction.
-
Arcs connecting the places and the transitions represent the relations between corresponding substances and interactions.
As described above, HFPNe model allows modeling and simulation of biological networks combining both an intuitive graphical representation and well-founded mathematic definition. Because of the versatility of HFPNe, it has been successfully employed to develop and analyze complex biological networks [7, 19, 20]. For example, in [7], Li et al. employed a series of generic places/transitions to realize 48 distinct genetic conditions that are the combination of four genes (lin12, lin15, vul and lst) and one anchor cell (AC) for determining the vulval precursor cell fate. AC, lin15, vul and lst can toggle between true and false. lin12 has three string-type values, i.e., "wt", "ko", "gf", indicating three genetic conditions of wild, knockout and overexpression of lin12 (refer to Figures seven and eight in [7]). Saito et al.[19] applied HFPNe to model regulatory networks that involve new key regulator microRNA. They selected the cell fate determination model of two gustatory neurons of Caenorhabditis elegans - ASE left (ASEL) and ASE right (ASER) (see Figure three in [19]). These neurons are morphologically bilaterally symmetric but physically asymmetric in function. By the simulation, they have confirmed the hypothesis that the cell fate is determined by the double-negative feedback loop involving lsy-6 and mir-273 microRNAs. Tasaki et al.[20] introduced time-series proteomic data to the HFPNe model. The authors semi-automatically constructed a well-tuned epidermal growth factor receptor signal transduction pathway model (EGFR model, see Figure two in [20]) coupled with their data assimilation (DA) framework.
Model Analysis
We present two new algorithms (i.e. Algorithm 1 and Algorithm 2) for analyzing structural transformation of HFPNe model over time. Figure 2 illustrates a schematic overview describing how to use Methods for the analysis based on time-course simulation data.
Algorithm to extract temporal subnet from time-course simulation data
First we show Algorithm 1 for extracting temporal subnets from time-course simulation data (simulation data for short). The simulation data is generated by using the simulator of HFPNe, which is saved in an expression data format (called EDF). In EDF, the concentrations of all places (i.e., the marking) are stored at every time point during the simulation (in this case, a constant time interval). Let  = x0x1⋯x
sim
be a non-empty list of simulation time points, where x0 is a start time point of the simulation and x
sim
is an end time point. The size (the number of elements) of the list
= x0x1⋯x
sim
be a non-empty list of simulation time points, where x0 is a start time point of the simulation and x
sim
is an end time point. The size (the number of elements) of the list  is denoted by |
is denoted by | |.
|.
Algorithm 1 aims to (i) extract a minimal element set of the HFPNe model at time x (i.e., the extracted set cannot be reduced furthermore). In other words, such a minimal element set with corresponding concentration distribution M(x), will return exactly the same simulation results as the original model under a precondition that the elapsed delay time of the discrete transition is given in the EDF. Any disturbance to the elements belonging to this minimal set will lead to different simulation results; and (ii) derive a total minimal element sets by exhaustively examining all reachable states of the HFPNe model with respect to the structural transformations along the time variations. We thus define temporal subnet H'(x) at time point x as such a minimal element set consisting of usable HFPNe elements involving:
-
(1)
enabled arcs;
-
(2)
transitions connected by (1); and
-
(3)
places connected by (1) and places connected from (2).
The temporal subnet H'(x i ) has following positive mathematical qualities: (i) the places involved in H'(x i ) is able to be simulated with corresponding concentration distribution M(x i ), and the simulation result of these places from x i to xi+1is exactly the same to the one of the original HFPNe model; and (ii) all elements in H'(x i ) take part in the firing at x i , i.e., corresponding biological components do participate in regulatory activity. We formalize this notion in the following definitions:
Definition 7. Let H = (P, T, A, τ, w, u, d) be an HFPNe.
-
(1)
Let p be a place in P, °p (or p°) is a set of the input (or output) transitions of p.
-
(2)
A Tis a set of the test arcs; A Iis a set of the inhibitory arcs; and A Nis a set of the normal input arcs.
-
(3)
For each arc c, let °c denote the source of c; let c° denote the target of c. □
Definition 8. Let t be a transition of the given HFPNe H.
-
(1)
°t is the set of the input places {pλ 1, pλ 2,⋯, pλ |°t|} of t; t° is the set of the output places {PO 1, PO 2, ⋯, PO |t°|} of t.
-
(2)
PT tis the set of the arcs from the places in °t to t; TP tis the set of the arcs from t to the places in t°.
-
(3)
The set of input places connected by the inhibitory arcs to the transition t is denoted as
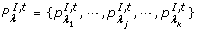 . A I, tis the set of the inhibitory arcs
. A I, tis the set of the inhibitory arcs 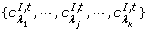
 . Similarly, the set of the test (or normal) arcs from the input places of t to t is denoted as A T, t(or A N, t).
. Similarly, the set of the test (or normal) arcs from the input places of t to t is denoted as A T, t(or A N, t). -
(4)
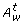 is the set of disabled normal and test arcs {c|(c∈(A T, t∪A N, t)) ∧ ((w(c)≥M [°c])∨(w(c) = false))}, where w(c) is the activity function.
is the set of disabled normal and test arcs {c|(c∈(A T, t∪A N, t)) ∧ ((w(c)≥M [°c])∨(w(c) = false))}, where w(c) is the activity function. 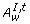 is the set of enabled inhibitory arcs {c|(c∈A I, t) ∧ ((w(c) < M [°c])∨(w(c) = true))}. □
is the set of enabled inhibitory arcs {c|(c∈A I, t) ∧ ((w(c) < M [°c])∨(w(c) = true))}. □
Algorithm 1. EXTRACTING TEMPORAL SUB NET
For a given HFPNe H = (P, T, A, τ, w, u, d) at time x, calculate TSN(H, x) and return H'(x).
TSN(H, x):
-
1.
H'←H
-
2.
RMVA(H') /* delete disabled arcs */
-
3.
RMVT(H') /* delete isolated transitions */
-
4.
RMVP(H') /* delete isolated places*/
-
5.
return H'
RMVA(H'):
For ∀t∈T of H',
1. if |A I, t | = 0 /* if there exists no inhibitory arc */
/* if there exists such a normal/test arc whose evaluated value of activity function is greater than or equal to the concentration of the connected place */
2. if delete PTt∪TPt
delete PTt∪TPt
3. else /* more than one inhibitory arc existing */
4. if
/* if there exists an inhibitory arc whose evaluated value of activity function is less than the concentration of the connected place */
5.if delete
delete  ∪TPt
∪TPt
6. else delete PTt∪TPt
7. else
8. if delete
delete  ∪TPt
∪TPt
9. else delete AI, t
RMVT(H'):
For ∀t∈T of H,
if ((PTt= ϕ) ∧ (TPt= ϕ)) delete t /* delete isolated transition */
RMVP(H'):
For ∀p∈P of H,
if ((°p = ϕ) ∧ (p° = ϕ)) delete p /* delete isolated place */
The above algorithm TSN(H, x) is composed of three parts: RMVA(H'), RMVT(H') and RMVP(H'). RMVA(H') is designed to eliminate disabled arcs. RMVT(H') and RMVP(H') are designed to eliminate isolated transitions and places respectively since such elements cannot participate in regulatory interactions. Figure 3 illustrates the processes of extracting temporal subnet H'(x) from H by applying the above algorithm with a given transition t. In Figure 3, inhibitory arc c2 has an evaluated value w(c2) less than the concentration M [°c2] of its connected place pλ2. That means (1) the inhibitory arc c2 represses the activity of transition t; and (2) two arcs c1 and  are disabled due to the inhibition via c2. These arcs are consequently deleted at step 5 in RMVA(H') (see the procedure from block (a) to (b)). Further, due to the inhibition from pλ2 which prevents the token amount from flowing into the place po1, the output arc a'(t, po1) of t is thus deleted in step 5. This results in three isolated places pλ1,
are disabled due to the inhibition via c2. These arcs are consequently deleted at step 5 in RMVA(H') (see the procedure from block (a) to (b)). Further, due to the inhibition from pλ2 which prevents the token amount from flowing into the place po1, the output arc a'(t, po1) of t is thus deleted in step 5. This results in three isolated places pλ1,  and po1 which are all deleted at step 4 in TSN(H, x) (see the procedure from block (b) to (c) in Figure 3). Time complexity of above algorithm to calculate an H for x is O(|A|+|T|+|P|), where O(|A|) is the time complexity of RMVA(H'). Likewise, O(|T|) is the time complexity of RMVT(H') and O(|P|) is the time complexity of RMVP(H'). By repeating the above algorithm to the list of simulation time points
and po1 which are all deleted at step 4 in TSN(H, x) (see the procedure from block (b) to (c) in Figure 3). Time complexity of above algorithm to calculate an H for x is O(|A|+|T|+|P|), where O(|A|) is the time complexity of RMVA(H'). Likewise, O(|T|) is the time complexity of RMVT(H') and O(|P|) is the time complexity of RMVP(H'). By repeating the above algorithm to the list of simulation time points  = x0x1⋯x
sim
based on the simulation data EDF, we can obtain a multiset
= x0x1⋯x
sim
based on the simulation data EDF, we can obtain a multiset  of all temporal subnets {H'(x0), H'(x1),⋯, H'(x
sim
)}.
of all temporal subnets {H'(x0), H'(x1),⋯, H'(x
sim
)}.
An example illustrating the process of performing Algorithm 1. For a given transition t, the processes of extracting a temporal subnet H'(x) from H at time x by applying Algorithm 1. Block (b) is obtained from (a) by performing the subroutine RMVA(H') (step 2 in TSN(H, x)). Block (c) is obtained from (b) by performing the subroutine RMVP(H') (step 4 in TSN(H, x)). Note that t is connected by an enabled inhibitory arc, therefore t cannot be removed by RMVT(H') (step 3 in TSN(H, x)) in Algorithm 1.
Building Active State Transition Diagram (ASTD)
We here show the other algorithm based on the outputs (i.e., temporal subnets) obtained in Algorithm 1. For a given time points list  and a set of temporal subnets
and a set of temporal subnets  obtained from Algorithm 1, by applying following Algorithm 2, we derive a directed graph, called active state transition diagram (ASTD), which is denoted by G = (N, E). N represents a set of distinct nodes {z1,⋯, z|N|}. Each node z∈N is called active subnet (ASN) (or state for short), extracted from the set of temporal subsets
obtained from Algorithm 1, by applying following Algorithm 2, we derive a directed graph, called active state transition diagram (ASTD), which is denoted by G = (N, E). N represents a set of distinct nodes {z1,⋯, z|N|}. Each node z∈N is called active subnet (ASN) (or state for short), extracted from the set of temporal subsets  without repetition. E denotes a set of directed edges e from z
i
to z
j
, represented by e = (z
i
, z
j
).
without repetition. E denotes a set of directed edges e from z
i
to z
j
, represented by e = (z
i
, z
j
).
Algorithm 2. CONSTRUCTING ACTIVE STATE TRANSITION DIAGRAM
x: current time point.
sid : state ID.
StateMap: a state map storing H'(x) as key and sid as value.
Gen(H'(x)): a function to output sid by referring to the state map.
curState: current state.
prevState: previous state.
sim: simulation time.
1. x←x 0, sid←1, z 1←H' (0), prevState←H'(0), N←{z 1}
2. insert (prevState, 1) to StateMap, push sid to FIFO queue Q
3. for i = 1 to sim
4. x←x i , curState←H'(x)
5. if (curState≠prevState)
6. if ({curState}∩N = ϕ)
7. sid++, z sid ← H'(x), N←N∪{z sid }
insert (curState, sid) to StateMap and push sid to Q
insert edge e = (zGen(prevState), z sid ) to E
8. else push Gen(curState) to Q and
insert edge e = (zGen(prevState), zGen(curState)) to E
9. prevState←curState
10 return G = (N, E)
In steps 1 and 2 of the above algorithm, we mainly build a state map storing temporal subnet H' (x) as key and state ID sid as value that is used as the suffix of node z∈N. The state map is employed to find the state ID sid by referring to the state map when using the function Gen(H'(x)). We also construct a FIFO queue Q to store the state ID in turn when reading the temporal subnet H(x') along the list of  (see Figure 2).
(see Figure 2).
In steps 3-9, the procedures are executed until x
sim
with a constant time interval to find out the ASNs among the temporal subnets  . In step 5, we compare current state with previous state, where current state indicates the temporal subnet H'(x
i
) and previous state indicates the temporal subnet H' (xi-1) at the previous time point.
. In step 5, we compare current state with previous state, where current state indicates the temporal subnet H'(x
i
) and previous state indicates the temporal subnet H' (xi-1) at the previous time point.
If H'(x
i
) is different from H'(xi-1), and a temporal subnet equivalent to H'(x
i
) does not exist in N, the current state H'(x
i
) will be treated as a new node z
sid
and the following procedures will be processed in step 7: (i) N←N∪{z
sid
}, (ii) insert (current state, state ID) to the state map StateMap and push sid to Q, and (iii) an edge e(H'(xi-1), H'(x
i
)) from previous state to current state is inserted to E. Otherwise if current state H'(x) already exists in N, we (i) push sid to Q, where sid is derived by referring to the state map via the function Gen(H' (x
i
)), and (ii) insert an edge from the previous state to the current state to E. Time complexity of Algorithm 2 is  .
.
In Figure 2, we can finally derive the ASTD G after performing Algorithm 2, where N = {z1, z2, z3} and E = {e1, e2}. Three distinct states (i.e., ASNs) z1, z2, z3 are derived from | | temporal subnets. It can be noticed that constructing ASTD can avoid redundancies in HFPNe structure, while retaining expressiveness of dynamic behaviors.
| temporal subnets. It can be noticed that constructing ASTD can avoid redundancies in HFPNe structure, while retaining expressiveness of dynamic behaviors.
In the next section, we demonstrate how to integrate and interpret the simulation data from circadian rhythm model in Drosophila to obtain a deeper understanding of structural and dynamic behaviors with ASTD.
Results
A case study: model of circadian clock
Biological background and modeling
There are five genes involved in the Drosophila circadian rhythm: period (per), timeless (tim), Drosophila Clock (dClk), cycle (cyc) and double-time (dbt). It has been known that the Drosophila circadian system is composed of two interlocked negative feedback loops: (i) Drosophila proteins PER and TIM form a heterodimer (PER/TIM) in the cytoplasm. After the nuclear translocation, PER/TIM inhibits the transcription of per and tim in a cycling negative feedback loop. Meanwhile, PER/TIM activates the transcription of dClk involved in the dCLK/CYC negative feedback loop; (ii) the proteins dCLK and CYC form a heterodimer dCLK/CYC that activates per and tim transcriptions and inhibits dClk transcription. Figure 4(a) shows the HFPNe model of wild type (called normal model) without external disturbances (e.g., light effects). With parameters shown in Figure 4(a), in silico simulation generated stable oscillations in mRNAs of three clock genes, tim, per, dClk, and proteins dCLK, CYC, dCLK/CYC, PER, TIM, DBT, PER/DBT, PER/TIM with periods as shown in Figure 4(b). The detailed mechanism is given in [21–23].
HFPNe model and its simulation result of circadian rhythm in Drosophila. (a) HFPNe model of circadian rhythm in Drosophila. The accompanying variable m x at a place represents the concentration of the corresponding mRNA, protein or the compound. For example, the variable m1 indicates the concentration of dClk mRNA. Reaction speed (the rate of transcription, translation, complex formation or degradation) is expressed by a simple formula at each transition. For example, the formula m1/5 indicates the translation rate of dCLK protein that depends on the variable m1 for the dClk Mrna concentration. The real number over an arc is the threshold for the content of the place attached to this arc. For example, the translation of tim mRNA occurs during the period that the place value of tim mRNA exceeds 1.0. (b) Oscillations of tim, per, dClk mRNAs, and the proteins TIM, PER, dCLK, PER/TIM, PER/DBT, dCLK/CYC (left y-axis) and DBT, CYC (right y-axis). The unit of x-axis is [pt] ([pt] is the virtual time unit of the HFPNe model), while that of y-axis is [vc] ([vc] is the virtual concentration unit).
Results and Discussion
[ASTD analysis of normal model]
This subsection presents the resulting ASTD from performing Algorithm 1 and Algorithm 2. The HFPNe model, simulation data and related data files of analyzing circadian rhythm model in Drosophila are available at the website [24]. In the simulation data, x
sim
is 150 [pt] with the time interval of 0.01 [pt] ([pt] is the virtual time unit of the HFPNe model). Figure 5 shows the resulting ASTD from processing the circadian time-course simulation data. The ASTD is derived by the following procedures: (i) By applying Algorithm 1 to the simulation data, we obtain the set of all the temporal subnets  . The total number of the set is 15,000 corresponding to 15,000 time points. As mentioned above, each temporal subnet is the minimal element set at time x; and next (ii) Applying Algorithm 2 to the outputs of Algorithm 1, we construct the ASTD.
. The total number of the set is 15,000 corresponding to 15,000 time points. As mentioned above, each temporal subnet is the minimal element set at time x; and next (ii) Applying Algorithm 2 to the outputs of Algorithm 1, we construct the ASTD.
Schematic representation of ASTDWand ASTDL. The four bold-line blocks of z19, z20, z10 and z11 on the left side show the corresponding temporal subnets that are the minimal element sets at respective time points. Dashed-line block shows the state transitions of "z19→z20→z10↔z11" in the ASTD and corresponding detailed regulation variations of HFPNe elements. For example, in the structural transformation from z19 to z20, two inhibitory arcs a(p13, t10) and a(p13, t14) are enabled due to the increase in the concentration of PER/TIM, resulting in the deletion of four arcs a(p5, t10), a(p5, t14), a'(t10, p6) and a'(t14, p8). Note that the transformation from z11 to z10 is omitted.
The constructed ASTD G = (N, E) of the normal model is composed of 24 unique nodes N={z1, z2,⋯, z24} connected by the black and green edges in E on the right side of Figure 5. Each node with a blue circle represents a state. The result demonstrates that our method successfully extracts 24 unique temporal subnets (i.e., ASNs) out of 15,000. This result suggests that (i) the number of all the temporal subnets of Drosophila circadian clock model can be reduced from 15,000 to only 24 when considering structural transformation due to the concentration variation, and further (ii) these 24 ASNs are all the states regulating the stable oscillations in the normal model. Each edge connected from previous state to current state denotes a direct structural transformation from the previous net structure to the current one. In Figure 5, dashed-line block is shown as an example to depict the state transitions of "z19→z20→z10↔z11" connected with the edges (z19, z20), (z20, z10), (z10, z11) and (z11, z10). Detailed direct structural transformations of HFPNe elements are illustrated in the left dashed-line block.
As an example we discuss the structural transformation from z19 to z20. Figures of the structural transformations of all the states along with corresponding ASTD are given as additional materials [see Additional files 2 and 3]. Due to an increase in PER/TIM concentration, two inhibitory arcs a(p13, t10) and a(p13, t14) are enabled (highlighted in pink), which results in the deletion of four arcs a(p5, t10), a(p5, t14), a'(t10, p6) and a'(t14, p8) (highlighted in blue). Meanwhile, a test arc from PER/TIM is also enabled, which results in the adding of arc a(t0, p1). It thus leads to a new temporal subnet structure regarded as z20 connected from the previous state z19. This captures the fact that in the Drosophila circadian clock model, the net structure in z20 can only transform from z19 on account of the rising of PER/TIM level. This restricts the reasonable transitions into state z20 to be z19, which simplifies analysis for both biologists and computational biologists.
The sparseness of this network will be of great value to computational biologists who need to rapidly investigating a range of regulatory interactions and dynamic behaviors from simulation data of their models. More detailedly, ASTD (i) gives researchers a concise impression of the connection relationship between the nodes. The nodes that researchers are interested in can be comprehensively focused and traced according to its connection in the ASTD; and (ii) such nodes can be further explored to explicitly elucidate the mechanism how the occurrence of structural transformation triggers oscillations along the time axis.
We also observe that state transitions from z1 to z9 are used only once, and are likely the period before the circadian rhythm systems reach a stable cycle from the initial marking. Excluding such nodes, the ASTD becomes only a cycle composed of the outer-ring nodes (i.e., all the nodes excluding {z1, z2,⋯, z9}). The state transfers following the cycle of these outer-ring nodes in the ASTD on the rhythms of mRNAs and proteins in this oscillation systems. In the following, we investigate how the ASTD changes when modifying the gene dbt.
[Mutant analysis]
Price et al. discussed the property of dbtL("L" for long) that is a mutation of dbt. They showed that the transcription of the gene per is affected by this mutant, i.e., the period of per mRNA in dbtLmutant is longer than the one in the normal model [23]. The behavior of per mRNA in dbtLmutant and normal model is validated afterwards by Matsuno et al.[22] (see Additional file 4 illustrating the simulation results). It is obtained by changing the formula at the transition (t23 = m7*m12/1000 in our case) denoting the complex forming rate of PER and DBT. Roughly speaking, when the forming rate of PER/DBT is slowed, it leaves more PER to bind to TIM, which leads to a faster increase of PER/TIM to a higher concentration. It thus will take longer time to inhibit the transcription of per mRNA and tim mRNA until the concentration of PER/TIM decreases to the respective threshold values of the inhibitor arcs (see Figure 4(a)). Therefore, the next increases of per mRNA and tim mRNA are accordingly postponed because of the longer inhibition effect resulting from the slow forming rate of PER/DBT. The results gave the suggestion that the circadian rhythm is controlled by this forming rate, which is affected by the mutant dbtL.
Due to the space limitation, we show the ASTD of dbtLmutant model (ASTDLfor short) in the figure together with the ASTD of the normal model (denoted as ASTDWfor short). Note that we employ the same mutant model in [22] for comparison. In Figure 5, the ASTDL(N, E) is composed of 23 distinct ASNs, where N = {z1, z2,⋯, z21, z24, z25} and E is the set of edges drawn in black and red. The resulting ASTDWand ASTDLgive information that the temporal structure of ASTDLis simpler than the one of ASTDWfrom the viewpoints of node number and connection relationship. Figure 5 also provides the information to generate following views: (i) shared 22 nodes {z1, z2,⋯, z21, z24} in ASTDWand ASTDLcontribute to produce oscillations regardless of the period length; and (ii) the temporal structures of disappeared z22 and z23 in ASTDLdo not contribute to the regulation of the forming rate of complex PER/DBT. In Additional files 2 and 3, it can be confirmed that the transitions t23 in z22 and z23 are both disabled (in grey), which reflects that no complex forming action occurs by the formula alteration in the mutant model.
[Graphical-based analyses of ASTD]
As described above, ASTD can give the user concise impression regarding the time-dependent structural changes in the pathway, which provides a great help in investigating a range of regulatory interactions and dynamic system behaviors. Additionally, it would be helpful to consider some more intuitive graphical representations to express the characteristic information from ASTD. With the help of such characteristics, one can obtain an intuitive understanding to the dynamic behaviors such as "Which state is maintained longer?", "How does the frequency of entering a certain state vary with the parameters?", and "How does the concentration of a substance vary in each state?"
We incorporate graphical representation applying to the states in the ASTD showing three characteristics: (i) duration, (ii) out-degree, and (iii) total concentration difference of substance in each state.
Firstly, duration is used to demonstrate the total persistence period of each state when it is reached. Node size of ASTD is then scaled up or down corresponding to the duration summation of each state. Secondly, out-degree is the number of edges going out of a node. This concept is employed to characterize the frequency of a certain node used in ASTD. Figure 6(a) displays the characterized ASTDWand ASTDLwith respect to the duration and out-degree. The scales of node sizes denoting duration and out-degree are given on the right-side of Figure 6(a), respectively. The node size of duration is according to the persistence time period of each node. The node size of out-degree is based on the calculation of natural log ln(count), where count is the number of edges going out of a node. We demonstrate how to analyze ASTD in general by using duration together with out-degree, as well as discussing obtained ASTDWand ASTDLof circadian rhythm in Drosophila shown in Figure 6(a) as follows:
-
(i)
When duration is "B" (B for the big size of the node) and the out-degree is "S" (S for the small size of the node), the state of such node (e.g., z 18 and z 19,) is maintained at a relative stable condition;
-
(ii)
When duration and out-degree are both "S", the state of such node (e.g., z 3 and z 13) is seldom-used during the simulation and is negligible. z 3 with both "S" duration and out-degree in ASTDWand ASTDL, is considered negligible. On the other hand, z 13 displays "B" duration and out-degree in ASTDLunlike in ASTDW. As shown in Additional file 4, per mRNA has a longer periodic oscillation in the mutant model than in the normal one. In ASTDL, the state z 15 is transformed from z 13 and z 14. Not only duration but also out-degree of z 14 in ASTDWand ASTDLare almost in the same size. But those of z 13 changed from "S" in the normal model to "L" in the mutant one, and the node size is closed to z 14. It can be considered that the temporal structure of z 13 contributes to the regulatory mechanism to generate longer periodic oscillations of per mRNA in the mutant model;
-
(iii)
The case of that duration is "S" and out-degree is "B" is not observed in this ASTD. Such nodes are highly unstable and trigger frequent structural transformations. This instability is likely the reason such nodes are not found in the stable oscillations of the circadian rhythm;
-
(iv)
When duration and out-degree are both "B", the state of such node (e.g., z 12 and z 14) is unstable, but it is likely such node is important to the regulation of the oscillations.
Note that the ASTD allows multiple edges between two nodes. Several bidirectional arcs are observed in the resulting ASTD, e.g., the arcs between z14 and z15, z21 and z23, which represent two states oscillates from one another. We examined there occurs a series of short-term tiny concentration vibrations of PER and dCLK around respective threshold values, which lead to the bidirectional arcs coming into being. For example, when the concentration of dCLK (p2) changes up and down around evaluated threshold value 1.0 of the arc (p2, t4), the states z14 and z15 will oscillates from one another. The results of out-degree in Figure 6(a) shows that the nodes connected with bidirectional arcs are relatively larger than others. These larger nodes reflecting unstable short-term tiny concentration vibrations are considered to contribute to the formation of the steady oscillation period (i.e., the cycle composed of the outer-ring nodes).
Finally, we investigate the dynamic behaviors of each substance's concentration level. We present this in a heat-map-like representation, where the total concentration difference is represented by colors as shown in Figure 6(b). The total difference in concentration level Diff Total (p, z) is the difference summation in place p' s concentration (M(p) [x i ]-M (p) [xi-1]) at adjacent time points in the given state z. Figure 6(b) compares concentration differences in per mRNA (p1) and dClk mRNA (p6). In tracking per mRNA, the nodes z17, z18 and z19 are colored in red around z18, while for dClk mRNA, the nodes z20, z10 and z11 are colored in red around z11. The shift states accurately reflect the difference in rise times for per and dClk mRNA level. Further, by investigating the temporal subnets in the ASTD, it is confirmed that the transition t10 denoting the transcription of per mRNA is enabled only in the red states z17, z18 and z19, while t10 is disabled in all the other states due to the inhibition of PER/TIM. Similarly, the transition t0 of dClk mRNA transcription is enabled in the red states z20, z10 and z11, while it is disabled in the others because of the inhibition by the dCLK/CYC complex. In this way, the information of each substance's relative expression can be easily visualized using ASTD with this characteristic.
Discussion
Investigating dynamic behaviors of biological networks is usually achieved by analyzing concentration plots of the simulation data. However, studying such concentration variations of a model generate more vital temporal structural information than considering dynamics as an ensemble. We thus proposed a novel techniques combines quantitative simulation data and topological analysis to deduce the dynamic behaviors of system mechanisms from the data. In this paper, we give a cycle ASTD of circadian rhythm of Drosophila from the simulation data as an example. ASTD can also be a linear succession of states, which is usually derived from the signaling pathway owing to its feature of propagating signals from transmembrane to the DNA nucleus. Such linear ASTD can also be employed as an analysis tool for quick interpretation. With the aid of graphical-based analyses, ASTD can yield concise impression of the connection relationship among the states from various viewpoints, such as time period, concentration variation and so on.
ASTD and reachability graph
ASTD is different from the concept of reachability graph (i.e., graph of markings) [25]. ASTD is made up of the nodes that are the unique temporal subnets, and of directed edges corresponding to the structural transformation of temporal subnets resulting in the passing from one state to another. Each node in ASTD is the grouping of identical temporal subnets from the viewpoint of structure. That is, each node simply possesses the structural information of the entries in the minimal element set that is extracted by eliminating the disabled transitions/arcs and isolated places. No concentration information (i.e., marking) is recorded in the ASTD (this is the point different from the concept of reachability graph) although such information is used to determine the ASTD. In contrast, reachability graph consists of nodes corresponding to reachable markings and of arcs corresponding to firing of transitions [25]. From this case study with the given sampling interval, the state space of reachability graph is 15,000, while that of ASTDLis significantly reduced to 24. A series of non-negative real numbers in the column of the EDF file is equivalent to current marking (state) in the reachability graph. Additionally, ASTD can deal with any general type, e.g., string and object. There are totally 15,000 unique markings obtained from EDF file. The state space of reachability graph will not be less than 15,000 when further decreasing the sampling interval time of simulation.
Conclusions
This paper describe a novel methodology to construct a so-called active state transition diagram (ASTD) by using the time-course simulation data from a well-founded formal framework of hybrid functional Petri net with extension (HFPNe). The main contributions are as follows: (i) Automatically constructed ASTD we have presented suggests that building an ASTD representation can eliminate redundant HFPNe structures, while maintaining equivalent expressiveness as the full model; (ii) Characterized ASTD gives the user concise impression and new insights to grasp and trace how a key regulatory subnet and/or a network changes with time; (iii) Due to the nature of the ASTD, any state belonging to the ASTD is able to be simulated and it enables us to simulate equivalent concentration distributions; and (iv) The applicability of the proposed method is investigated by the analysis of an HFPNe model of circadian rhythm in Drosophila.
Another approach to represent biochemical reactions as a system is to use a series of ordinary differential equations (ODEs). Since the HFPNe allows quantities to be continuous and generic, the biological processes with ODE-based kinetics can be realized [22], i.e., an ODE-based system that is convertible into an HFPNe model, can yield an ASTD and give simplified graphical representation of the time-dependent structural transformation. There is, however, a special case at this point, for models without inhibitory arcs and with threshold value of normal and test arcs equal to zero, the resulting ASTDs will contain only one state - a full HFPNe structure - for all the time points. Moreover, for the ODE model of hybrid dynamical systems, an existing method has been developed providing a mathematical approach with applying reachability analysis by Halász et al.[16]. It serves as a promising theoretic basis and leads us to make further investigation on this special case as the future work.
In this paper, the circadian rhythm model of Drosophila is a deterministic one, in which all the parameters of transition speeds and arc thresholds have been determined in advance [22]. Since HFPNe model supports stochastic transitions as well, in the future, ASTD will be adapted to such probabilistic features of the system as well as the firing conflict problem of the discrete transition by means of particular graphical-based representation. Additionally, building ASTD makes possible converting a hybrid model dealing with discrete, continuous and more complicated events to finite time-dependent states. Various analysis techniques, e.g., network motif analysis, centrality analysis, clustering analysis and model checking technique, will also be imported to the ASTD to obtain better understanding of systematic dynamics from simulation data as the future research.
References
Chaouiya C: Petri net modelling of biological networks. Brief Bioinform. 2007, 8 (4): 210-219.
Koch I, Heiner M: Petri nets. Analysis of Biological Networks. Edited by: Junker BH, Schreiber F. 2008, 139-180. A Wiley Interscience Publication,
Chen M, Hofestädt R: Quantitative Petri net model of gene regulated metabolic networks in the cell. In Silico Biol. 2003, 3 (3): 347-365.
Koch I, Junker BH, Heiner M: Application of Petri net theory for modelling and validation of the sucrose breakdown pathway in the potato tuber. Bioinformatics. 2005, 21 (7): 1219-1226.
Ruths D, Muller M, Tseng JT, Nakhleh L, Ram PT: The signaling petri net-based simulator: a non-parametric strategy for characterizing the dynamics of cell-specific signaling networks. PLoS Comput Biol. 2008, 4 (2):
Sackmann A, Formanowicz D, Formanowicz P, Blazewicz J: New insights into the human body iron metabolism analyzed by a Petri net based approach. Biosystems. 2009, 96 (1): 104-113.
Li C, Nagasaki M, Ueno K, Miyano S: Simulation-based model checking approach to cell fate specification during Caenorhabditis elegans vulval development by hybrid functional Petri net with extension. BMC Syst Biol. 2009, 3 (42):
Steggles LJ, Banks R, Shaw O, Wipat A: Qualitatively modelling and analysing genetic regulatory networks: a Petri net approach. Bioinformatics. 2007, 23 (3): 336-343.
Nagasaki M, Saito A, Li C, Jeong E, Miyano S: Systematic reconstruction of TRANSPATH data into Cell System Markup Language. BMC Syst Biol. 2008, 2 (53):
Krull M, Voss N, Choi C, Pistor S, Potapov A, Wingender E: TRANSPATH: an integrated database on signal transduction and a tool for array analysis. Nucleic Acids Res. 2003, 31 (1): 97-100.
Zevedei-Oancea I, Schuster S: Topological analysis of metabolic networks based on Petri net theory. In Silico Biol. 2003, 3 (3): 323-345.
Grafahrend-Belau E, Schreiber F, Heiner M, Sackmann A, Junker BH, Grunwald S, Speer A, Winder K, Koch I: Modularization of biochemical networks based on classification of Petri net t-invariants. BMC Bioinformatics. 2008, 9 (90):
Heiner M, Koch I, Will J: Model validation of biological pathways using Petri nets, demonstrated for apoptosis. Biosystems. 2004, 75 (1-3): 15-28.
Li C, Suzuki S, Ge QW, Nakata M, Matsuno H, S M: Structural modeling and analysis of signaling pathways based on Petri nets. J Bioinform Comput Biol. 2006, 4 (5): 1119-1140.
Hardy S, Robillard PN: Petri net-based method for the analysis of the dynamics of signal propagation in signaling pathways. Bioinformatics. 2008, 24 (2): 209-217.
Halász A, Kumar V, Imieliński M, Belta C, Sokolsky O, Pathak S, Rubin H: Analysis of lactose metabolism in E. Coli using reachability analysis of hybrid systems. IET Syst Biol. 2007, 1 (2): 130-148.
Nagasaki M, Doi A, Matsuno H, Miyano S: A versatile Petri net based architecture for modeling and simulation of complex biological processes. Genome Inform. 2004, 15 (1): 180-197.
Peterson JL: Petri Net Theory and the Modeling of Systems. 1981, Prentice Hall,
Saito A, Nagasaki M, Doi A, Ueno K, Miyano S: Cell fate simulation model of gustatory neurons with MicroRNAs double-negative feedback loop by hybrid functional Petri net with extension. Genome Inform. 2006, 17 (1): 100-111.
Tasaki S, Nagasaki M, Oyama M, Hata H, Ueno K, Yoshida R, Higuchi T, Sugano S, Miyano S: Modeling and estimation of dynamic EGFR pathway by data assimilation approach using time series proteomic data. Genome Inform. 2006, 17 (2): 226-238.
Kloss B, Price JL, Saez L, Blau J, Rothenfluh A, Wesley CS, Young MW: The Drosophila clock gene double-time encodes a protein closely related to human casein Kinase Iepsilon. Cell. 1998, 94: 97-107.
Matsuno H, Tanaka Y, Aoshima H, Doi A, Matsui M, Miyano S: Biopathways representation and simulation on hybrid functional Petri net. In Silico Biol. 2003, 3 (3): 389-404.
Price JL, Blau J, Rothenfluh A, Abodeely M, Kloss B, Young MW: Double-time is a novel Drosophila clock gene that regulates PERIOD protein accumulation. Cell. 1998, 94 (1): 83-95.
ASTD of Drosophila Circadian rhythm model.http://www.csml.org/models/csml-models/circadian-rhythms-in-drosophila/ASTD/
David R, Alla H: Discrete, Continuous, and Hybrid Petri Nets. 2004, Springer,
Acknowledgements
We are grateful to the anonymous reviewers for their valuable hints and suggestions. This work was supported by KAKENHI (Grant-in-Aid for Scientific Research) on Priority Areas "Systems Genomics" from the Ministry of Education, Culture, Sports, Science and Technology of Japan.
Author information
Authors and Affiliations
Corresponding author
Additional information
Authors' contributions
The basic idea was considered by MN and further developed by CL and MN. MN implemented proposed method, and CL wrote the draft of the manuscript. The most of the figures are made by AS. CL, MN and AS evaluated the resulting ASTD. SM supervised the whole study. The final manuscript was read and approved by all authors.
Chen Li, Masao Nagasaki contributed equally to this work.
Electronic supplementary material
12918_2009_428_MOESM1_ESM.PDF
Additional file 1:Definition of hybrid functional Petri net with extension (HFPNe). The data provide full mathematical definitions of HFPNe. (PDF 43 KB)
12918_2009_428_MOESM3_ESM.PDF
Additional file 3:Detailed net structure of all the nodes in the resulting ASTD. Detailed net structure of all 25 nodes (note that one node is displayed in one page). Readers can turn page forward and back to see the structural difference between two nodes in an easy-to-understand manner. (PDF 469 KB)
12918_2009_428_MOESM4_ESM.PDF
Additional file 4:Concentration behaviors of per mRNA: (a) normal model; and (b) dbtLmutant. Formula such as m7* m12/1000 for the firing speed of transition t23 is given at charts (a) and (b), which represents complex forming rate of two proteins PER and DBT. The firing speed in dbtLis slower than the one in the normal model. (PDF 105 KB)
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
Open Access This article is published under license to BioMed Central Ltd. This is an Open Access article is distributed under the terms of the Creative Commons Attribution License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Li, C., Nagasaki, M., Saito, A. et al. Time-dependent structural transformation analysis to high-level Petri net model with active state transition diagram. BMC Syst Biol 4, 39 (2010). https://doi.org/10.1186/1752-0509-4-39
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1752-0509-4-39


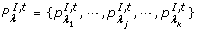 . A I, tis the set of the inhibitory arcs
. A I, tis the set of the inhibitory arcs 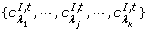
 . Similarly, the set of the test (or normal) arcs from the input places of t to t is denoted as A T, t(or A N, t).
. Similarly, the set of the test (or normal) arcs from the input places of t to t is denoted as A T, t(or A N, t).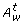 is the set of disabled normal and test arcs {c|(c
is the set of disabled normal and test arcs {c|(c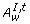 is the set of enabled inhibitory arcs {c|(c
is the set of enabled inhibitory arcs {c|(c


